题目内容
7. 如图,斜线段AB与平面α所成的角为60°,B为斜足,平面α上的动点P满足∠PAB=30°,则点P的轨迹是椭圆.
如图,斜线段AB与平面α所成的角为60°,B为斜足,平面α上的动点P满足∠PAB=30°,则点P的轨迹是椭圆.
分析 根据题意,∠PAB=30°为定值,可得点P的轨迹为一以AB为轴线的圆锥侧面与平面α的交线,则答案可求.
解答 解:用垂直于圆锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面和圆锥的一条母线平行时,得到抛物线.
此题中平面α上的动点P满足∠PAB=30°,可理解为P在以AB为轴的圆锥的侧面上,
再由斜线段AB与平面α所成的角为60°,可知P的轨迹符合圆锥曲线中椭圆定义.
故可知动点P的轨迹是椭圆.
故答案为:椭圆.
点评 本题考查椭圆的定义,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
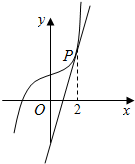 如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.
如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.