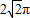题目内容
(9分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点.
(1)求直线BE与平面ABCD所成角的正切值;
(2)在侧面PAB内找一点N,使NE⊥面PAC,
并求出N点到AB和AP的距离.

【答案】
(1)直线BE与平面ABCD所成角的正切值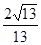 .
.
(2)N点到AB的距离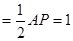 ,N点到AP的距离
,N点到AP的距离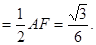
【解析】解:方法一、(1)取AD中点F,连接EF、BF,则EF//PA,
由侧棱PA⊥底面ABCD,∴EF⊥底面ABCD,则∠EBF为BE与
平面ABCD所成角
∴在△EBF中,EF=1,BF= ,tan∠EBF=
,tan∠EBF=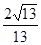
即直线BE与平面ABCD所成角的正切值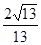 .
.
(2)在面ABCD内过D作AC的垂线交AB于F,则 .
.
连PF,则在Rt△ADF中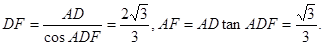
设N为PF的中点,连NE,则NE//DF,
∵DF⊥AC,DF⊥PA,∴DF⊥面PAC,从而NE⊥面PAC.
∴N点到AB的距离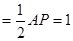 ,N点到AP的距离
,N点到AP的距离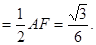

练习册系列答案
相关题目
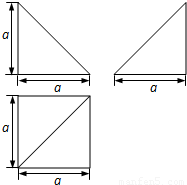
 (2012•邯郸模拟)四棱锥P-ABCD的五个顶点都在一个球面上,其三视图如图所示,E、F分别是棱AB、CD的中点,直线EF被球面所截得的线段长为
(2012•邯郸模拟)四棱锥P-ABCD的五个顶点都在一个球面上,其三视图如图所示,E、F分别是棱AB、CD的中点,直线EF被球面所截得的线段长为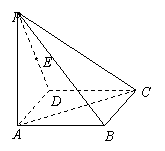 (2)在侧面PAB内找一点N,使NE⊥面PAC,
(2)在侧面PAB内找一点N,使NE⊥面PAC,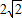 ,则该球表面积为( )
,则该球表面积为( )
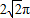
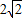 ,则该球表面积为( )
,则该球表面积为( )