题目内容
四棱锥P-ABCD的五个顶点都在一个球面上,其三视图如图所示,E、F分别是棱AB、CD的中点,直线EF被球面所截得的线段长为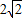 ,则该球表面积为( )
,则该球表面积为( )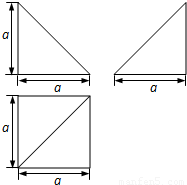
A.9π
B.3π
C.
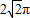
D.12π
【答案】分析:将三视图还原为直观图,得四棱锥P-ABCD的五个顶点位于同一个正方体的顶点处,且与该正方体内接于同一个球.由此结合题意,可得正方体的棱长为2,算出外接球半径R,再结合球的表面积公式,即可得到该球表面积.
解答:解:将三视图还原为直观图如右图,可得四棱锥P-ABCD的五个顶点位于同一个正方体的顶点处,
且与该正方体内接于同一个球.且该正方体的棱长为a
设外接球的球心为O,则O也是正方体的中心,设EF中点为G,连接OG,OA,AG
根据题意,直线EF被球面所截得的线段长为2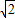 ,即正方体面对角线长也是2
,即正方体面对角线长也是2 可得AG=
可得AG= =
=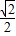 a,所以正方体棱长a=2
a,所以正方体棱长a=2
∴Rt△OGA中,OG= a=1,AO=
a=1,AO=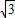
即外接球半径R= ,得外接球表面积为4πR2=12π
,得外接球表面积为4πR2=12π
故选D.
点评:本题主要考查了将三视图还原为直观图,并且求外接球的表面积,着重考查了正方体的性质、三视图和球内接多面体等知识,属于中档题.
解答:解:将三视图还原为直观图如右图,可得四棱锥P-ABCD的五个顶点位于同一个正方体的顶点处,
且与该正方体内接于同一个球.且该正方体的棱长为a

设外接球的球心为O,则O也是正方体的中心,设EF中点为G,连接OG,OA,AG
根据题意,直线EF被球面所截得的线段长为2
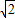 ,即正方体面对角线长也是2
,即正方体面对角线长也是2 可得AG=
可得AG= =
=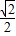 a,所以正方体棱长a=2
a,所以正方体棱长a=2∴Rt△OGA中,OG=
 a=1,AO=
a=1,AO=
即外接球半径R=
 ,得外接球表面积为4πR2=12π
,得外接球表面积为4πR2=12π故选D.
点评:本题主要考查了将三视图还原为直观图,并且求外接球的表面积,着重考查了正方体的性质、三视图和球内接多面体等知识,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
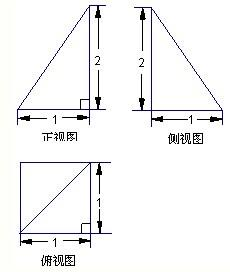 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
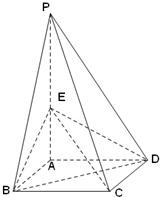 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: