题目内容
已知椭圆E的中心在原点,焦点在x轴上,离心率为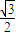 ,且过抛物线C:x2=4y的焦点F.
,且过抛物线C:x2=4y的焦点F.(I)求椭圆E的方程;
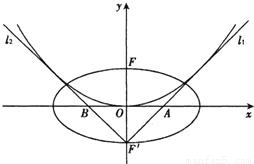
(II)过坐标平面上的点F'作拋物线c的两条切线l1和l2,它们分别交拋物线C的另一条切线l3于A,B两点.
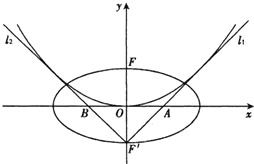
(i)若点F′恰好是点F关于-轴的对称点,且l3与拋物线c的切点恰好为拋物线的顶点(如图),求证:△ABF′的外接圆过点F;
(ii)试探究:若改变点F′的位置,或切线l3的位置,或抛物线C的开口大小,(i)中的结论是否仍然成立?由此给出一个使(i)中的结论成立的命题,并加以证明.
【答案】分析:(I)根据椭圆的离心率为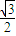 ,可得,
,可得, =
=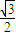 ,根据椭圆过抛物线C:x2=4y的焦点F.可知点F(0,1)满足椭圆方程,再根据a2=b2+c2,即可求出a,b,c,得出椭圆方程.
,根据椭圆过抛物线C:x2=4y的焦点F.可知点F(0,1)满足椭圆方程,再根据a2=b2+c2,即可求出a,b,c,得出椭圆方程.
(II)(i)只要能求出△ABF′的外接圆方程,再验证点F是否在圆上,命题就得证.可先求出三条切线方程,分别联立,求三条切线交点,再利用待定系数法求△ABF′的外接圆方程,最后,把F点坐标代入,看是否满足方程即可.
(ii)命题可写出几个,选最好证明的写,不妨写成:设F′为抛物线外一点,若过点F'作拋物线c的两条切线l1和l2,分别交拋物线C的另一条切线l3于A,B两点,则:△ABF′的外接圆过抛物线的焦点F.仿照(i),把三条切线方程设出,分别联立,求三个交点坐标,再证,F′,A,B,F四点共圆,来证明命题.
解答:解:(I)由已知得F(0,1),设椭圆方程为 (a>b>0),则,b=1
(a>b>0),则,b=1
椭圆的离心率为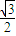 ,可得,
,可得,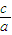 =
=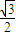 ,又∵a2=b2+c2,∴a=2,c=
,又∵a2=b2+c2,∴a=2,c=
∴椭圆方程为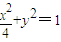
(II)(i)依题意,点F′的坐标为(0,-1),过点F'且与拋物线c相切的直线斜率存在,
设其方程为y=kx-1.代入抛物线方程,消y,得x2-4kx+4=0,令△=0,得k=±1
则切线l1和l2方程分别为y=x-1和y=-x-1,又∵且l3与拋物线c的切点恰好为拋物线的顶点.
∴l3的方程为y=0.
由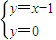 ,得点A坐标为(1,0)
,得点A坐标为(1,0)
由 ,得点B坐标为(-1,0)
,得点B坐标为(-1,0)
设△ABF′′的外接圆方程为x2+y2+Dx+Ey+4F=0,则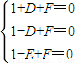 ,解得
,解得
∴设△ABF′′的外接圆方程为x2+y2=1
:△ABF′的外接圆过抛物线的焦点F.
(ii)使(i)中的结论成立的命题为:设F′为抛物线外一点,若过点F'作拋物线c的两条切线l1和l2,分别交拋物线C的另一条切线l3于A,B两点,则△ABF′的外接圆过抛物线的焦点F.
证明:不妨设拋物线方程为x2=2py,li分别与抛物线交于点Pi(xi,yi)(i=1,2,3)
依题意,x1,x2,x3中至少有两个不为0,不妨设x1≠0,x2≠0.
∵ 故切线li的方程为y-yi=
故切线li的方程为y-yi= (x-xi),i=1,2,3
(x-xi),i=1,2,3
由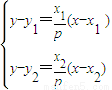 ,得F′(
,得F′(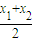 ,
,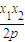 )
)
由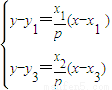 得A(
得A( 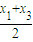 ,
,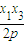 )
)
 ,得B(
,得B( 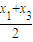 ,
, )
)
∴AF′的垂直平分线方程为y- =-
=- (x-
(x-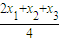 ),
),
BF′ 的垂直平分线方程为 y-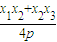 =-
=- (x-
(x-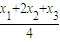 )
)
它们的交点为M(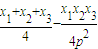 ,
, )
)
又∵F(0,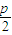 ),AF的中点为N(
),AF的中点为N(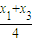 ,
,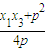 )
)
从而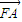 =(
=( 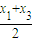 ,
, ),
),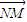 =(
=( 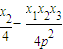 ,
, )
)
 =
=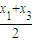 (
( )+
)+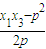 •
• =0
=0
∴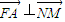 ,∴AF′,BF′AF的垂直平分线教育一点M圆上,即△ABF′的外接圆过抛物线的焦点F.
,∴AF′,BF′AF的垂直平分线教育一点M圆上,即△ABF′的外接圆过抛物线的焦点F.
点评:本题考查了直线与抛物线的位置关系,题目较难,须认真考虑.
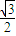 ,可得,
,可得, =
=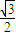 ,根据椭圆过抛物线C:x2=4y的焦点F.可知点F(0,1)满足椭圆方程,再根据a2=b2+c2,即可求出a,b,c,得出椭圆方程.
,根据椭圆过抛物线C:x2=4y的焦点F.可知点F(0,1)满足椭圆方程,再根据a2=b2+c2,即可求出a,b,c,得出椭圆方程.(II)(i)只要能求出△ABF′的外接圆方程,再验证点F是否在圆上,命题就得证.可先求出三条切线方程,分别联立,求三条切线交点,再利用待定系数法求△ABF′的外接圆方程,最后,把F点坐标代入,看是否满足方程即可.
(ii)命题可写出几个,选最好证明的写,不妨写成:设F′为抛物线外一点,若过点F'作拋物线c的两条切线l1和l2,分别交拋物线C的另一条切线l3于A,B两点,则:△ABF′的外接圆过抛物线的焦点F.仿照(i),把三条切线方程设出,分别联立,求三个交点坐标,再证,F′,A,B,F四点共圆,来证明命题.
解答:解:(I)由已知得F(0,1),设椭圆方程为
 (a>b>0),则,b=1
(a>b>0),则,b=1椭圆的离心率为
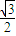 ,可得,
,可得,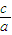 =
=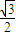 ,又∵a2=b2+c2,∴a=2,c=
,又∵a2=b2+c2,∴a=2,c=
∴椭圆方程为
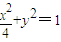
(II)(i)依题意,点F′的坐标为(0,-1),过点F'且与拋物线c相切的直线斜率存在,
设其方程为y=kx-1.代入抛物线方程,消y,得x2-4kx+4=0,令△=0,得k=±1
则切线l1和l2方程分别为y=x-1和y=-x-1,又∵且l3与拋物线c的切点恰好为拋物线的顶点.
∴l3的方程为y=0.
由
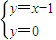 ,得点A坐标为(1,0)
,得点A坐标为(1,0)由
 ,得点B坐标为(-1,0)
,得点B坐标为(-1,0)设△ABF′′的外接圆方程为x2+y2+Dx+Ey+4F=0,则
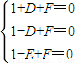 ,解得
,解得
∴设△ABF′′的外接圆方程为x2+y2=1
:△ABF′的外接圆过抛物线的焦点F.
(ii)使(i)中的结论成立的命题为:设F′为抛物线外一点,若过点F'作拋物线c的两条切线l1和l2,分别交拋物线C的另一条切线l3于A,B两点,则△ABF′的外接圆过抛物线的焦点F.
证明:不妨设拋物线方程为x2=2py,li分别与抛物线交于点Pi(xi,yi)(i=1,2,3)
依题意,x1,x2,x3中至少有两个不为0,不妨设x1≠0,x2≠0.
∵
 故切线li的方程为y-yi=
故切线li的方程为y-yi= (x-xi),i=1,2,3
(x-xi),i=1,2,3由
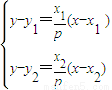 ,得F′(
,得F′(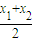 ,
,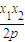 )
)由
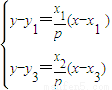 得A(
得A( 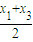 ,
,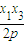 )
)  ,得B(
,得B( 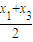 ,
, )
)∴AF′的垂直平分线方程为y-
 =-
=- (x-
(x-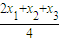 ),
),BF′ 的垂直平分线方程为 y-
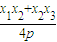 =-
=- (x-
(x-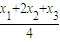 )
)它们的交点为M(
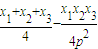 ,
, )
)又∵F(0,
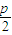 ),AF的中点为N(
),AF的中点为N(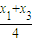 ,
,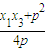 )
)从而
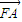 =(
=( 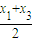 ,
, ),
),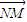 =(
=( 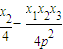 ,
, )
) =
=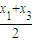 (
( )+
)+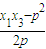 •
• =0
=0 ∴
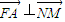 ,∴AF′,BF′AF的垂直平分线教育一点M圆上,即△ABF′的外接圆过抛物线的焦点F.
,∴AF′,BF′AF的垂直平分线教育一点M圆上,即△ABF′的外接圆过抛物线的焦点F.点评:本题考查了直线与抛物线的位置关系,题目较难,须认真考虑.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 已知椭圆E的中心在原点,焦点在x轴上,离心率为
已知椭圆E的中心在原点,焦点在x轴上,离心率为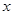 轴上,椭圆上的点到两个焦点的距离之和为
轴上,椭圆上的点到两个焦点的距离之和为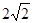 ,离心率
,离心率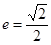
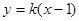 交椭圆E于点P、Q,且OP^OQ。求实数k的值.
交椭圆E于点P、Q,且OP^OQ。求实数k的值.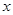 轴上,椭圆上的点到两个焦点的距离之和为
轴上,椭圆上的点到两个焦点的距离之和为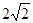 ,离心率
,离心率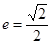
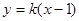 交椭圆E于点P、Q,且OP^OQ。求实数k的值.
交椭圆E于点P、Q,且OP^OQ。求实数k的值.