题目内容
已知椭圆E的中心在原点,焦点在x轴上,椭圆上的点到焦点的距离的最小值为| 2 |
| ||
| 2 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点(1,0)作直线l交E于P、Q两点,试问在x轴上是否存在一定点M,使
| MP |
| MQ |
分析:(Ⅰ)
?
,由此能导出所求椭圆E的方程.
(Ⅱ)当直线l不与x轴重合时,可设直线l的方程为:x=ky+,由1
,整理得:(k2+2)y2+2ky-1=0,
,假设存在定点M(m,0),使得
•
为定值.由此入手能够推导出存在定点M(
,0),使得对于经过(1,0)点的任意一条直线l均有
•
=-
(恒为定值).
|
|
(Ⅱ)当直线l不与x轴重合时,可设直线l的方程为:x=ky+,由1
|
|
|
| MP |
| MQ |
| 5 |
| 4 |
| MP |
| MQ |
| 7 |
| 16 |
解答:解:(Ⅰ)
?
,
∴所求椭圆E的方程为:
+y2=1(5分)
(Ⅱ)当直线l不与x轴重合时,可设直线l的方程为:x=ky+1
,
把(2)代入(1)整理得:(k2+2)y2+2ky-1=0(3)
∴
,(8分)
假设存在定点M(m,0),使得
•
为定值
•
=(x1-m,y1)•(x2-m,y2)=(x1-m)(x2-m)+y1y2
=(ky1+1-m)(ky2+1-m)+y1y2=(k2+1)y1y2+k(1-m)(y1+y2)+(1-m)2=-
-
+(1-m)2=
+(1-m)2=
+(1-m)2
当且仅当5-4m=0,即m=
时,
•
=-
(为定值).这时M(
,0)(12分)
再验证当直线l的倾斜角α=0时的情形,此时取P(-
,0),Q(
,0)
=(-
-
,0),
=(
-
,0)
•
=(-
-
)•(
-
)=-
∴存在定点M(
,0)使得对于经过(1,0)点的任意一条直线l均有
•
=-
(恒为定值).
|
|
∴所求椭圆E的方程为:
| x2 |
| 2 |
(Ⅱ)当直线l不与x轴重合时,可设直线l的方程为:x=ky+1
|
|
把(2)代入(1)整理得:(k2+2)y2+2ky-1=0(3)
∴
|
假设存在定点M(m,0),使得
| MP |
| MQ |
| MP |
| MQ |
=(ky1+1-m)(ky2+1-m)+y1y2=(k2+1)y1y2+k(1-m)(y1+y2)+(1-m)2=-
| (k2+1) |
| k2+2 |
| 2k2(1-m) |
| k2+2 |
| (2m-3)k2-1 |
| k2+2 |
| (2m-3)(k2+2)+(5-4m) |
| k2+2 |
当且仅当5-4m=0,即m=
| 5 |
| 4 |
| MP |
| MQ |
| 7 |
| 16 |
| 5 |
| 4 |
再验证当直线l的倾斜角α=0时的情形,此时取P(-
| 2 |
| 2 |
| MP |
| 2 |
| 5 |
| 4 |
| MQ |
| 2 |
| 5 |
| 4 |
| MP |
| MQ |
| 2 |
| 5 |
| 4 |
| 2 |
| 5 |
| 4 |
| 7 |
| 16 |
∴存在定点M(
| 5 |
| 4 |
| MP |
| MQ |
| 7 |
| 16 |
点评:本题考查椭圆方程的求法和点M的存在性质的判断.解题时要认真审题,注意挖掘题设中的隐含条件,灵活运用椭圆的性质,合理地进行等价转化.

练习册系列答案
相关题目
 已知椭圆E的中心在原点,焦点在x轴上,离心率为
已知椭圆E的中心在原点,焦点在x轴上,离心率为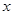 轴上,椭圆上的点到两个焦点的距离之和为
轴上,椭圆上的点到两个焦点的距离之和为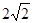 ,离心率
,离心率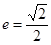
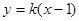 交椭圆E于点P、Q,且OP^OQ。求实数k的值.
交椭圆E于点P、Q,且OP^OQ。求实数k的值.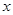 轴上,椭圆上的点到两个焦点的距离之和为
轴上,椭圆上的点到两个焦点的距离之和为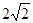 ,离心率
,离心率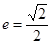
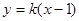 交椭圆E于点P、Q,且OP^OQ。求实数k的值.
交椭圆E于点P、Q,且OP^OQ。求实数k的值.