题目内容
设函数![]()
(Ⅰ)求![]() 的单调区间及极小值;
的单调区间及极小值;
(Ⅱ)确定方程![]() 的根的一个近似值,使其误差不超过0.5,并说明理由
的根的一个近似值,使其误差不超过0.5,并说明理由
(Ⅲ)当![]() 时,证明:对任意的实数x>2,恒有
时,证明:对任意的实数x>2,恒有![]()
解:(1)由![]() ,
,
![]()
![]() 的单调增区间为
的单调增区间为![]() 单调减区间为
单调减区间为![]()
当x=2时有极小值![]() -----------------------------------4分
-----------------------------------4分
(2)由(1)知![]() 上单调递增,又
上单调递增,又![]()
![]() 知方程
知方程![]() 只有一个实根
只有一个实根![]() ,
,![]()
故取![]() 的近似值3.5满足所需的误差要求。-----------------------8分
的近似值3.5满足所需的误差要求。-----------------------8分
(3)![]()
记![]() ,所以
,所以![]() 单调递增。因为
单调递增。因为![]()
当![]()
所以当![]() 从而命题得证。-----------12分
从而命题得证。-----------12分

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
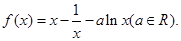
 的单调性;
的单调性;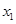 和
和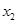 ,记过点
,记过点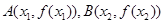 的直线的斜率为
的直线的斜率为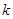 ,问:是否存在
,问:是否存在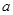 ,使得
,使得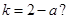 若存在,求出
若存在,求出
 的单调性;
的单调性; ,记过点
,记过点 的直线的斜率为
的直线的斜率为 ,问:是否存在
,问:是否存在 ,使得
,使得 若存在,求出
若存在,求出 ,当
,当 时,
时, .
. 且
且 ,求
,求 的单增区间.
的单增区间.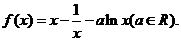
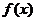 的单调性;
的单调性;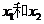 ,记过点
,记过点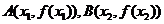 的直线的斜率为
的直线的斜率为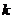 ,问:是否存在
,问:是否存在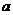 ,使得
,使得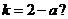 若存在,求出
若存在,求出