题目内容
设函数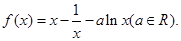
(I)讨论 的单调性;
的单调性;
(II)若 有两个极值点
有两个极值点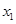 和
和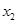 ,记过点
,记过点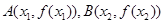 的直线的斜率为
的直线的斜率为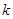 ,问:是否存在
,问:是否存在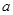 ,使得
,使得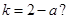 若存在,求出
若存在,求出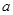 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】
(I)(1)当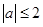 时
时 ,
,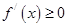 故
故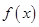 在
在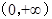 上单调递增 ;
上单调递增 ;
(2)当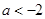 时
时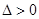 ,
,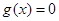 的两根都小于
的两根都小于 ,在
,在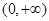 上,
上,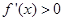 ,
,
故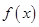 在
在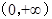 上单调递增;
上单调递增;
(3)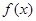 分别在
分别在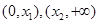 上单调递增,在
上单调递增,在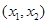 上单调递减.
上单调递减.
(II)不存在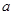 ,使得
,使得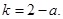
【解析】
试题分析:(I)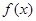 的定义域为
的定义域为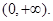
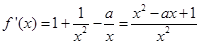 1分
1分
令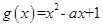 ,其判别式
,其判别式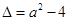 2分
2分
(1)当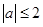 时
时 ,
,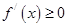 故
故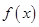 在
在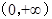 上单调递增
3分
上单调递增
3分
(2)当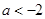 时
时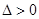 ,
,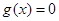 的两根都小于
的两根都小于 ,在
,在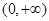 上,
上,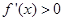 ,
,
故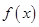 在
在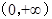 上单调递增
4分
上单调递增
4分
(3)当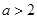 时
时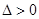 ,
,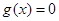 的两根为
的两根为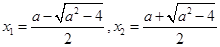 ,
,
当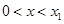 时,
时, 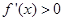 ;当
;当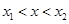 时,
时, 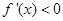 ;当
;当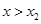 时,
时, 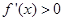 ,故
,故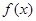 分别在
分别在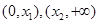 上单调递增,在
上单调递增,在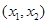 上单调递减.
6分
上单调递减.
6分
(II)由(I)知,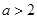 .因为
.因为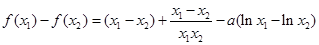 ,
,
所以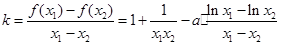 7分
7分
又由(I)知,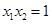 .于是
.于是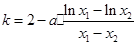 8分
8分
若存在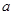 ,使得
,使得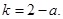 则
则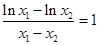 .即
.即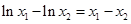 .
9分
.
9分
亦即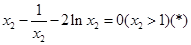 0分
0分
再由(I)知,函数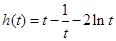 在
在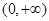 上单调递增,
11分
上单调递增,
11分
而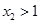 ,所以
,所以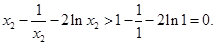 这与
这与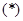 式矛盾.
式矛盾.
故不存在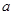 ,使得
,使得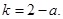 12分
12分
考点:本题主要考查导数的几何意义,应用导数研究函数的单调性、极值,存在性问题探讨。
点评:典型题,本题属于导数应用中的基本问题,通过研究函数的单调性,明确了极值情况。通过研究函数的单调区间,得到直线斜率表达式。存在性问题,往往要假设存在,利用已知条件探求。本题涉及对数函数,要特别注意函数的定义域。

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目

 的单调性;
的单调性; 和
和 ,记过点
,记过点 的直线的斜率为
的直线的斜率为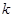 ,问:是否存在
,问:是否存在 ,使得
,使得 ?若存在,求出
?若存在,求出
 的单调性;
的单调性; 和
和 ,记过点
,记过点 的直线的斜率为
的直线的斜率为 ,问:是否存在
,问:是否存在 ,使得
,使得 ?若存在,求出
?若存在,求出
 的单调性;
的单调性; ,记过点
,记过点 的直线的斜率为
的直线的斜率为 ,问:是否存在
,问:是否存在 ,使得
,使得 若存在,求出
若存在,求出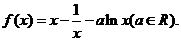
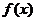 的单调性;
的单调性;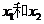 ,记过点
,记过点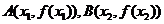 的直线的斜率为
的直线的斜率为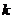 ,问:是否存在
,问:是否存在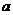 ,使得
,使得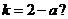 若存在,求出
若存在,求出