题目内容
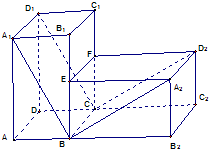 已知,在水平平面α上有一长方体AC1绕BC旋转90°得到如图1所示的几何体.
已知,在水平平面α上有一长方体AC1绕BC旋转90°得到如图1所示的几何体.(Ⅰ)证明:平面BCD1A1⊥平面BCD2A2;
(Ⅱ)当BC=1时,且长方体AC1体积为4时,求四棱锥A1-BCD2A2体积的最小值.
分析:(I)欲证平面BCD1A1⊥平面BCD2A2,只需在平面BCD1A1内找一直线垂直平面BCD2A2,而A1B⊥BA2,BC⊥A1B,BC∩BA2=B,满足线面垂直的判定定理,从而A1B⊥平面BCD2A2,A1B?平面BCD1A1,满足面面垂直的判定定理;
(II)设AB=a,AA1=b,四棱锥A1-BCD2A2的体积为V,根据长方体AC1的体积为4,则ab=4,V=
×BC×BA2×A1B然后利用基本不等式求出最小值,即可求出所求,注意等号成立的条件.
(II)设AB=a,AA1=b,四棱锥A1-BCD2A2的体积为V,根据长方体AC1的体积为4,则ab=4,V=
| 1 |
| 3 |
解答:证明(I)证明:∵△A1BB1≌△EBA2,
∴∠A1BB1=∠BA2E,
∵∠BA2E+∠EBA2=90°,
∴∠A1BB1+∠EBA2=90°,
即 A1B⊥BA2
又∵BC⊥A1B(2分)
∵BC∩BA2=B
∴A1B⊥平面BCD2A2,(4分)
又∵A1B?平面BCD1A1(5分)
∴平面BCD1A1⊥平面BCD2A2(6分)
(II)设AB=a,AA1=b,四棱锥A1-BCD2A2的体积为V,
∵长方体AC1的体积为4,
∴ab=4,(7分)
由(1)知,A1B⊥平面BCD2A2,
∴V=
×BC×BA2×A1B=
×1×
×
=
(a2+b2)≥
ab=
,(10分)
当且仅当a=b=2时,等号成立,(11分)
所以四棱锥A1-BCD2A2的体积的最小值为
.(12分)
∴∠A1BB1=∠BA2E,
∵∠BA2E+∠EBA2=90°,
∴∠A1BB1+∠EBA2=90°,
即 A1B⊥BA2
又∵BC⊥A1B(2分)
∵BC∩BA2=B
∴A1B⊥平面BCD2A2,(4分)
又∵A1B?平面BCD1A1(5分)
∴平面BCD1A1⊥平面BCD2A2(6分)
(II)设AB=a,AA1=b,四棱锥A1-BCD2A2的体积为V,
∵长方体AC1的体积为4,
∴ab=4,(7分)
由(1)知,A1B⊥平面BCD2A2,
∴V=
| 1 |
| 3 |
| 1 |
| 3 |
| a2+b2 |
| a2+b2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
当且仅当a=b=2时,等号成立,(11分)
所以四棱锥A1-BCD2A2的体积的最小值为
| 8 |
| 3 |
点评:本题主要考查了面面垂直的判定,以及锥体的体积的度量,同时考查了论证推理能力,属于中档题.

练习册系列答案
相关题目
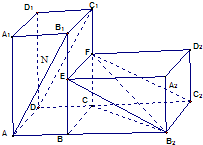 已知,在水平平面α上有一长方体AC1绕BC旋转900得到如图所示的几何体.
已知,在水平平面α上有一长方体AC1绕BC旋转900得到如图所示的几何体. 上有一长方体
上有一长方体 绕
绕 旋转
旋转 得到如图所示的几何体.
得到如图所示的几何体.
 平面
平面 ;
; 时,直线
时,直线 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ,求
,求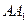 的长度;
的长度; 与平面
与平面 ,
, 长方体
长方体 ,请直接写出
,请直接写出 上有一长方体
上有一长方体 绕
绕 旋转
旋转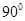 得到如图所示的几何体.
得到如图所示的几何体.
 平面
平面 ;
; 时,直线
时,直线 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ,求
,求 的长度;
的长度; 与平面
与平面 ,长方体
,长方体 ,请直接写出
,请直接写出 上有一长方体
上有一长方体 绕
绕 旋转
旋转 得到如图所示的几何体.
得到如图所示的几何体.
 平面
平面 ;
; 时,直线
时,直线 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ,求
,求 的长度;
的长度; 与平面
与平面 ,长方体
,长方体 ,请直接写出
,请直接写出