题目内容
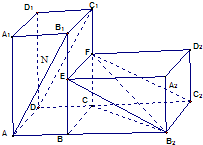 已知,在水平平面α上有一长方体AC1绕BC旋转900得到如图所示的几何体.
已知,在水平平面α上有一长方体AC1绕BC旋转900得到如图所示的几何体.(Ⅰ)证明:平面ADC1B1⊥平面EFC2B2;
(Ⅱ)当AB=BC=1时,直线CB2与平面ADC1B1所成的角的正弦值为
| 3 | 4 |
(Ⅲ)在(Ⅱ)条件下,设旋转过程中,平面BCC1B1与平面α所成的角为θ,长方体AC1的最高点离平面α的距离为f(θ),请直接写出f(θ)的一个表达式,并注明定义域.
分析:(Ⅰ) 延长B2E交AB1于N,利用平面几何知识证出AB1⊥B2E,再结合EF⊥AB1,可证出平面AB1⊥平面EFC2B2,从而证出平面ADC1B1⊥平面EFC2B2.
(Ⅱ)以CB1,CC2,CC1所在直线为x轴,y轴,z轴,建立空间直角坐标系C-xyz,设AA1=a 利用向量的方法表示出
与面ADC1B1所成的角的正弦值 通过解方程解决.
(Ⅲ)旋转过程中,平面BCC1B1与平面α所成的角为θ=∠B1BB2,最高点为A1,离平面α的距离是△A1BB2边BB2上的高,在△A1BB2中表示出即可.
(Ⅱ)以CB1,CC2,CC1所在直线为x轴,y轴,z轴,建立空间直角坐标系C-xyz,设AA1=a 利用向量的方法表示出
| CB2 |
(Ⅲ)旋转过程中,平面BCC1B1与平面α所成的角为θ=∠B1BB2,最高点为A1,离平面α的距离是△A1BB2边BB2上的高,在△A1BB2中表示出即可.
解答: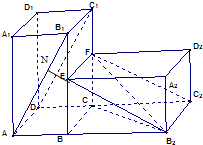 解:(Ⅰ)证明:延长B2E交AB1于N,
解:(Ⅰ)证明:延长B2E交AB1于N,
∵△ABB1≌△EBB2,
∴∠AB1B=∠EB2B,
∵∠AB1B+∠B1AB=90°,
∴∠EB2B+∠B1AB=90°,
∴∠ANB2=90°
即 AB1⊥B2E
又∵EF⊥AB1∵EF∩B2E=E
∴AB1⊥平面EFC2B2
又∵AB1?平面ADC1B1,
∴平面ADC1B1⊥平面EFC2B2;
(Ⅱ)如图,以CB1,CC2,CC1所在直线为x轴,y轴,z轴,建立空间直角坐标系C-xyz,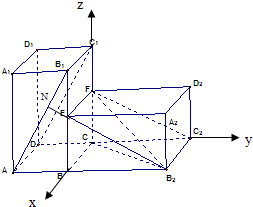
设AA1=a
∵AB=BC=1,则B2(1,a,0),A(1,-1,0),D(0,-1,0),B1(1,0,a)
∴
=(-1,0,0),
=(0,1,a),
=(1,a,0),
设平面ADC1B1的一个法向量为
=(x,y,z),
则由
⇒
,取
=(0,a,-1)
设直线CB1与平面ADC1B1所成的角为θ,则sinθ=|cos<
,
>|=
=
解得a=
(Ⅲ)f(θ)=2sin(θ+
),(0≤θ≤
)
 解:(Ⅰ)证明:延长B2E交AB1于N,
解:(Ⅰ)证明:延长B2E交AB1于N,∵△ABB1≌△EBB2,
∴∠AB1B=∠EB2B,
∵∠AB1B+∠B1AB=90°,
∴∠EB2B+∠B1AB=90°,
∴∠ANB2=90°
即 AB1⊥B2E
又∵EF⊥AB1∵EF∩B2E=E
∴AB1⊥平面EFC2B2
又∵AB1?平面ADC1B1,
∴平面ADC1B1⊥平面EFC2B2;
(Ⅱ)如图,以CB1,CC2,CC1所在直线为x轴,y轴,z轴,建立空间直角坐标系C-xyz,

设AA1=a
∵AB=BC=1,则B2(1,a,0),A(1,-1,0),D(0,-1,0),B1(1,0,a)
∴
| AD |
| AB1 |
| CB2 |
设平面ADC1B1的一个法向量为
| n |
则由
|
|
| n |
设直线CB1与平面ADC1B1所成的角为θ,则sinθ=|cos<
| n |
| CB2 |
| a2 | ||||
|
| 3 |
| 4 |
解得a=
| 3 |
(Ⅲ)f(θ)=2sin(θ+
| π |
| 6 |
| π |
| 2 |
点评:本题考查面面位置关系、线面角的度量、空间距离的表示,考查分析解决问题、空间想象、转化、计算的能力与方程思想.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
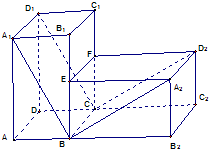 已知,在水平平面α上有一长方体AC1绕BC旋转90°得到如图1所示的几何体.
已知,在水平平面α上有一长方体AC1绕BC旋转90°得到如图1所示的几何体. 上有一长方体
上有一长方体 绕
绕 旋转
旋转 得到如图所示的几何体.
得到如图所示的几何体.
 平面
平面 ;
; 时,直线
时,直线 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ,求
,求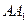 的长度;
的长度; 与平面
与平面 ,
, 长方体
长方体 ,请直接写出
,请直接写出 上有一长方体
上有一长方体 绕
绕 旋转
旋转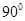 得到如图所示的几何体.
得到如图所示的几何体.
 平面
平面 ;
; 时,直线
时,直线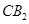 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ,求
,求 的长度;
的长度; 与平面
与平面 ,长方体
,长方体 ,请直接写出
,请直接写出 上有一长方体
上有一长方体 绕
绕 旋转
旋转 得到如图所示的几何体.
得到如图所示的几何体.
 平面
平面 ;
; 时,直线
时,直线 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ,求
,求 的长度;
的长度; 与平面
与平面 ,长方体
,长方体 ,请直接写出
,请直接写出