题目内容
已知真命题:“函数y=f(x)的图象关于点P(a,b)成中心对称图形”的充要条件为“函数y=f(x+a)-b 是奇函数”.(1)将函数g(x)=x3-3x2的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数g(x)图象对称中心的坐标;
(2)求函数h(x)=
 图象对称中心的坐标.
图象对称中心的坐标.
【答案】分析:(1)根据函数图象的平移变换法则,求出平移后函数的解析式,并根据奇偶性的性质判断函数为奇函数,结合题目中已知的真命题,可得答案.
(2)设函数h(x)=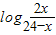 图象对称中心为P(a,b),由题设知函数f(x)=h(x+a)-b是奇函数.根据奇函数定义域对称及定义可求出a,b的值,得到对称中心坐标.
图象对称中心为P(a,b),由题设知函数f(x)=h(x+a)-b是奇函数.根据奇函数定义域对称及定义可求出a,b的值,得到对称中心坐标.
解答:解:(1)将函数g(x)=x3-3x2的图象向左平移1个单位,再向上平移2个单位,
平移后图象对应的函数解析式为y=(x+1)3-3(x+1)2+2=x3-3x,
由于函数y=x3-3x是奇函数,
由题设真命题知,函数g(x)图象对称中心的坐标是(1,-2).
(2)设函数h(x)=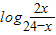 图象对称中心为P(a,b),
图象对称中心为P(a,b),
由题设知函数f(x)=h(x+a)-b是奇函数.
则f(x)=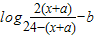 .由不等式
.由不等式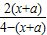 >0的解集关于原点对称,得a=2.
>0的解集关于原点对称,得a=2.
此时f(x)=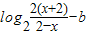 ,x∈(-2,2).
,x∈(-2,2).
任取x∈(-2,2),
由f(-x)+f(x)=0,得b=1,
所以函数函数h(x)=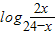 图象对称中心为P(2,1)
图象对称中心为P(2,1)
点评:本题考查的知识点是函数图象与图象变化,奇偶函数图象的对称性,熟练掌握函数图象平移变换法则及奇函数的定义和性质是解答的关键.
(2)设函数h(x)=
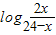 图象对称中心为P(a,b),由题设知函数f(x)=h(x+a)-b是奇函数.根据奇函数定义域对称及定义可求出a,b的值,得到对称中心坐标.
图象对称中心为P(a,b),由题设知函数f(x)=h(x+a)-b是奇函数.根据奇函数定义域对称及定义可求出a,b的值,得到对称中心坐标.解答:解:(1)将函数g(x)=x3-3x2的图象向左平移1个单位,再向上平移2个单位,
平移后图象对应的函数解析式为y=(x+1)3-3(x+1)2+2=x3-3x,
由于函数y=x3-3x是奇函数,
由题设真命题知,函数g(x)图象对称中心的坐标是(1,-2).
(2)设函数h(x)=
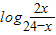 图象对称中心为P(a,b),
图象对称中心为P(a,b),由题设知函数f(x)=h(x+a)-b是奇函数.
则f(x)=
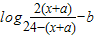 .由不等式
.由不等式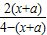 >0的解集关于原点对称,得a=2.
>0的解集关于原点对称,得a=2.此时f(x)=
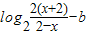 ,x∈(-2,2).
,x∈(-2,2).任取x∈(-2,2),
由f(-x)+f(x)=0,得b=1,
所以函数函数h(x)=
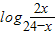 图象对称中心为P(2,1)
图象对称中心为P(2,1)点评:本题考查的知识点是函数图象与图象变化,奇偶函数图象的对称性,熟练掌握函数图象平移变换法则及奇函数的定义和性质是解答的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
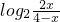 图象对称中心的坐标.
图象对称中心的坐标.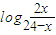 图象对称中心的坐标;
图象对称中心的坐标;