题目内容
(本小题满分12分)已知函数![]() .(1)若函数在区间
.(1)若函数在区间![]() (其中
(其中![]() )上存在极值,求实数a的取值范围;(2)如果当
)上存在极值,求实数a的取值范围;(2)如果当![]() 时,不等式
时,不等式![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
解析:
(1)因为![]() ,
,![]() ,则
,则![]() ………1分
………1分
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减,
上单调递减,
∴函数![]() 在
在![]() 处取得极大值. …………………………………3分
处取得极大值. …………………………………3分
∵函数![]() 在区间
在区间![]() (其中
(其中![]() )上存在极值,
)上存在极值,
∴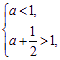 解得
解得![]() . ……………………….5分
. ……………………….5分
(2)不等式![]() ,即为
,即为![]() , ……………7分
, ……………7分
记![]() ,∴
,∴![]() ,
,
……………………………………9分
令![]() ,则
,则![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上递增,
上递增,
∴![]() ,从而
,从而![]() ,故
,故![]() 在
在![]() 上也单调递增,
上也单调递增,
∴![]() ,∴
,∴![]() . ……………………………12分
. ……………………………12分

练习册系列答案
相关题目