题目内容
11.在△ABC中,内角A,B,C所对边的长分别为a,b,c,且满足2bcosB=acosC+ccosA,若b=$\sqrt{3}$,则a+c的最大值为( )| A. | $2\sqrt{3}$ | B. | 3 | C. | $\frac{3}{2}$ | D. | 9 |
分析 利用正弦定理化边为角,可求导cosB,由此可得B,由余弦定理可得:3=a2+c2-ac,由基本不等式可得:ac≤3,代入:3=(a+c)2-3ac可得a+c的最大值.
解答 解:2bcosB=ccosA+acosC,
由正弦定理,得2sinBcosB=sinCcosA+sinAcosC,
∴2sinBcosB=sinB,
又sinB≠0,
∴cosB=$\frac{1}{2}$,
∴B=$\frac{π}{3}$.
∵由余弦定理可得:3=a2+c2-ac,
∴可得:3≥2ac-ac=ac,
∴即有:ac≤3,代入:3=(a+c)2-3ac可得:(a+c)2=3+3ac≤12,
∴a+c的最大值为2$\sqrt{3}$.
故选:A.
点评 该题考查正弦定理、余弦定理及其应用,基本不等式的应用,考查学生运用知识解决问题的能力,属于中档题.

练习册系列答案
相关题目
2.函数y=$\left\{\begin{array}{l}{3^x},x∈(-∞,1]\\ 3-\frac{3}{x},x∈(1,+∞)\end{array}$的值域为( )
| A. | (0,3) | B. | (0,3] | C. | (0,+∞) | D. | [0,+∞) |
1.已知命题P:?x0∈R,tanx0≥1,则它的否定为( )
| A. | ?x∈R,tanx≥1 | B. | ?x0∈R,tanx0>1 | C. | ?x∈R,tanx<1 | D. | ?x0∈R,tanx0<1 |
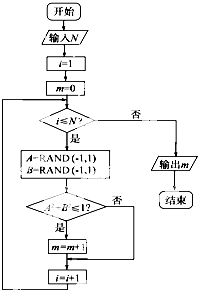 如图所示的程序框图可用来估计π的值(假设函数RAND(-1,1)是产
如图所示的程序框图可用来估计π的值(假设函数RAND(-1,1)是产