题目内容
10. 如图,设平面α与β相交于直线l,AC⊥α,BD⊥β,垂足分别为C、D,直线AB⊥AC,AB⊥BD.
如图,设平面α与β相交于直线l,AC⊥α,BD⊥β,垂足分别为C、D,直线AB⊥AC,AB⊥BD.求证:AB∥l.
分析 过A作AE⊥β,垂足为E,证明AB⊥平面ACE,l⊥平面ACE,即可证明结论.
解答 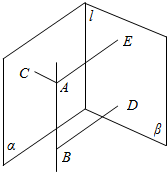 证明:∵平面α与β相交于直线l,AC⊥α,BD⊥β,
证明:∵平面α与β相交于直线l,AC⊥α,BD⊥β,
∴AC⊥l,BD⊥l,
过A作AE⊥β,垂足为E,则AE∥BD,
∵AB⊥BD,
∴AB⊥AE,
∴AB⊥平面ACE,
∵AE⊥β,∴AE⊥l,
∵AC⊥l,AE∩AC=A,
∴l⊥平面ACE,
∴AB∥l.
点评 本题考查线面垂直的判定与性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
20.已知两条直线l1:x+m2y+12=0和l2:(m-2)x+3my+4m=0,则l1∥l2是m=-1的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
18.已知等差数列{an}与{bn},它们的前n项和分别为Sn,Tn,若$\frac{{S}_{n}}{{T}_{n}}$=$\frac{2n-2}{n+3}$,则$\frac{{a}_{5}}{{b}_{5}}$=( )
| A. | 1 | B. | $\frac{5}{6}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
5.做直线运动的质点在任意位置x处,所受的力F(x)=1-e-x,则质点从x1=0,沿x轴运动到x2=1处,力F(x)所做的功是( )
| A. | e | B. | $\frac{1}{e}$ | C. | 2e | D. | $\frac{1}{2e}$ |
 已知奇函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-mx(x>0)}\\{0(x=0)}\\{{x}^{2}+2x(x<0)}\end{array}\right.$
已知奇函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-mx(x>0)}\\{0(x=0)}\\{{x}^{2}+2x(x<0)}\end{array}\right.$