题目内容
记f(x)=loga| 1+x |
| 1-x |
(Ⅰ)若关于x的方程:loga
| t |
| (1-x)(2x2-5x+5) |
(Ⅱ)当a=e(e是自然对数的底数)时,记h(x)=g(x)-
| x |
| 2 |
(Ⅲ)当a>1时,求证:
| n |
 |
| k=1 |
| lna |
| 2(a-1) |
分析:(Ⅰ)求出g(x),loga
=f(x)在[2,6]上有实数解,求出t的表达式,利用导数确定t 的范围;
(Ⅱ)a=e求出 h(x)=g(x)-
(x≥0),利用导数推出是增函数,求出最小值,即可求函数h(x)的最大值;
(Ⅲ)利用放缩法,求出
g(a-k)的取值范围,最后推出小于
即可.
| t |
| (1-x)(2x2-5x+5) |
(Ⅱ)a=e求出 h(x)=g(x)-
| x |
| 2 |
(Ⅲ)利用放缩法,求出
| n |
 |
| k=1 |
| lna |
| 2(a-1) |
解答:解:(Ⅰ)由条件可知:t=(1+x)(2x2-5x+5),在x∈[0,1)上有解.
t'=6x(x-1),当x∈[0,1)时,t'(x)<0,所以t(x)在[0,1)上单调递减.t(1)<t(x)≤t(0),即4<t≤5.(4分)
(Ⅱ)f(x)的定义域为(-1,1),g(x)=f-1(x)=
(x∈R),
当a=e时,h(x)=
-
(x≥0),所以h′(x)=
≤0,
所以h(x)在[0,+∞)上单调递减.所以,x≥0时,h(x)max=h(0)=0;(8分)
(Ⅲ)由(Ⅱ)的启示可以设G(x)=g(x)-
x,(x≥0)
则G′(x)=g′(x)-
=
≤0,
所以G(x)在[0,+∞)上单调递减,
当x>0时,G(x)<G(0)=0,即g(x)<
x
所以
g(a-k)<
(
+
++
)=
.
<
.(16分)
t'=6x(x-1),当x∈[0,1)时,t'(x)<0,所以t(x)在[0,1)上单调递减.t(1)<t(x)≤t(0),即4<t≤5.(4分)
(Ⅱ)f(x)的定义域为(-1,1),g(x)=f-1(x)=
| ax-1 |
| ax+1 |
当a=e时,h(x)=
| ex-1 |
| ex+1 |
| x |
| 2 |
| -(ex-1)2 |
| 2(ex+1)2 |
所以h(x)在[0,+∞)上单调递减.所以,x≥0时,h(x)max=h(0)=0;(8分)
(Ⅲ)由(Ⅱ)的启示可以设G(x)=g(x)-
| lna |
| 2 |
则G′(x)=g′(x)-
| lna |
| 2 |
| -(ax-1)2lna |
| (ax+1)2 |
所以G(x)在[0,+∞)上单调递减,
当x>0时,G(x)<G(0)=0,即g(x)<
| lna |
| 2 |
所以
| n |
 |
| k=1 |
| lna |
| 2 |
| 1 |
| a |
| 1 |
| a2 |
| 1 |
| an |
| lna |
| 2 |
1-
| ||
| a-1 |
| lna |
| 2(a-1) |
点评:本小题考查函数、反函数、方程、不等式、导数及其应用等基础知识,考查化归、分类整合等数学思想方法,以及推理论证、分析与解决问题的能力.

练习册系列答案
相关题目
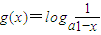 ,记F(x)=2f(x)+g(x)
,记F(x)=2f(x)+g(x)