题目内容
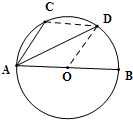
如图,AB是⊙O的直径,点C,D是半圆弧AB的两个三等分点,
=
,
=
,则
=( )
| AB |
| a |
| AC |
| b |
| AD |

A.
| B.
| C.
| D.
|
连结CD、OD,
∵点C、D是半圆弧AB的两个三等分点,
∴弧AC=弧BD,可得CD∥AB,∠CAD=∠DAB=
×90°=30°,
∵OA=OD
ADO=∠DAO=30°,
由此可得∠CAD=∠DAO=30°,
∴AC∥DO.
∴四边形ACDO为平行四边形,可得
=
+
,
∵
=
=
,
=
,
∴
=
+
.
故选:D

∵点C、D是半圆弧AB的两个三等分点,
∴弧AC=弧BD,可得CD∥AB,∠CAD=∠DAB=
| 1 |
| 3 |
∵OA=OD
ADO=∠DAO=30°,
由此可得∠CAD=∠DAO=30°,
∴AC∥DO.
∴四边形ACDO为平行四边形,可得
| AD |
| AO |
| AC |
∵
| AO |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| a |
| AC |
| b |
∴
| AD |
| 1 |
| 2 |
| a |
| b |
故选:D


练习册系列答案
相关题目
 是
是 的三条高,求证:
的三条高,求证:
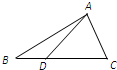
 中,若
中,若 ,则
,则 的值( )
的值( )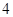 B.
B. C
C D.
D.
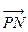 =-2
=-2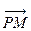 ,则P点的坐标为( )
,则P点的坐标为( )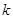 a+b与2 a-b互相垂直,则
a+b与2 a-b互相垂直,则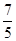
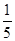
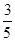
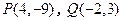 ,则直线
,则直线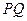 与
与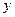 轴的交点分有向线段
轴的交点分有向线段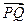 的比为 。
的比为 。