题目内容
函数y=log2(x-1)+ 的定义域为
的定义域为
- A.{x|x≥0}
- B.{x|x≥1}
- C.{x|x>1}
- D.{x|0≤x≥1}
C
分析:使该函数有意义,需要对数的真数大于0,同时需要根号下的代数式大于等于0,.
解答:要使原函数有意义,只需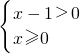 解得x>1,所以原函数的定义域为{x|x>1}.
解得x>1,所以原函数的定义域为{x|x>1}.
故选C.
点评:本题考查了函数定义域的求法,解答的关键是使构成函数式的每一部分都要有意义,属基础题.
分析:使该函数有意义,需要对数的真数大于0,同时需要根号下的代数式大于等于0,.
解答:要使原函数有意义,只需
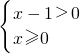 解得x>1,所以原函数的定义域为{x|x>1}.
解得x>1,所以原函数的定义域为{x|x>1}.故选C.
点评:本题考查了函数定义域的求法,解答的关键是使构成函数式的每一部分都要有意义,属基础题.

练习册系列答案
相关题目
函数y=log2(1+x)+
的定义域为( )
| 2-x |
| A、(0,2) |
| B、(-1,2] |
| C、(-1,2) |
| D、[0,2] |