题目内容
设椭圆 的左右焦点分别为
的左右焦点分别为 、
、 ,
, 是椭圆
是椭圆 上的一点,且
上的一点,且 ,坐标原点
,坐标原点 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆 的方程;
的方程;
(2) 设 是椭圆
是椭圆 上的一点,过点
上的一点,过点 的直线
的直线 交
交 轴于点
轴于点 ,交
,交 轴于点
轴于点 ,若
,若 ,求直线
,求直线 的斜率.
的斜率.
【答案】
解: (Ⅰ)由题设知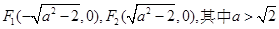
由于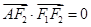 ,则有
,则有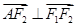 , A
, A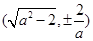 ……..2分
……..2分
故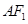 所在直线方程为
所在直线方程为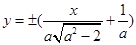 …………3分
…………3分
所以坐标原点 到直线
到直线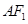 的距离为
的距离为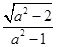 ,
,
又 ,所以
,所以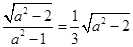 ,解得:
,解得: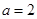 .…….5分
.…….5分
所求椭圆的方程为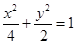 .…………6分
.…………6分
(2)由题意可知直线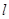 的斜率存在,设直线斜率为
的斜率存在,设直线斜率为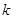 ,则直线
,则直线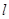 的方程为
的方程为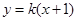 ,
,
则有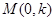 .……7分
.……7分
设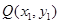 ,由于
,由于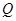 、
、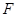 、
、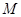 三点共线,且
三点共线,且 .
.
根据题意得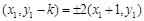 ,解得
,解得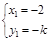 或
或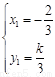 .……10分
.……10分
又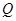 在椭圆
在椭圆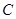 上,故
上,故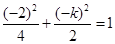 或
或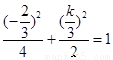 ,解得
,解得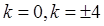 ,
,
综上,直线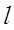 的斜率为
的斜率为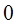 或
或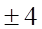 …………12分
…………12分
【解析】略

练习册系列答案
相关题目

 设椭圆
设椭圆 的左右焦点分别为
的左右焦点分别为 ,离心率
,离心率 ,点
,点 在直线
在直线 :
: 的左侧,且F2到l的距离为
的左侧,且F2到l的距离为 。
。 的值;
的值; 是
是 ,证明:当
,证明:当 取最小值时,
取最小值时, 。
。