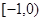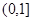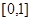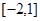题目内容
已知函数f(x)=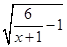 的定义域为集合A,函数g(x)=lg(-x2+2x+m)的定义域为集合B.
的定义域为集合A,函数g(x)=lg(-x2+2x+m)的定义域为集合B.
(1)当m=3时,求A∩(∁RB);
(2)若A∩B={x|-1<x<4},求实数m的值.
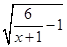 的定义域为集合A,函数g(x)=lg(-x2+2x+m)的定义域为集合B.
的定义域为集合A,函数g(x)=lg(-x2+2x+m)的定义域为集合B.(1)当m=3时,求A∩(∁RB);
(2)若A∩B={x|-1<x<4},求实数m的值.
(1){x|3≤x≤5}(2)8
A={x|-1<x≤5},
(1)当m=3时,B={x|-1<x<3},
则∁RB={x|x≤-1或x≥3},
∴A∩(∁RB)={x|3≤x≤5}.
(2)∵A={x|-1<x≤5},A∩B={x|-1<x<4},
故4是方程-x2+2x+m=0的一个根,
∴有-42+2×4+m=0,解得m=8.
此时B={x|-2<x<4},符合题意.
因此实数m的值为8.
(1)当m=3时,B={x|-1<x<3},
则∁RB={x|x≤-1或x≥3},
∴A∩(∁RB)={x|3≤x≤5}.
(2)∵A={x|-1<x≤5},A∩B={x|-1<x<4},
故4是方程-x2+2x+m=0的一个根,
∴有-42+2×4+m=0,解得m=8.
此时B={x|-2<x<4},符合题意.
因此实数m的值为8.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 ),则图中阴影部分所表示的集合为
),则图中阴影部分所表示的集合为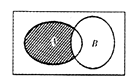
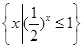 ,B=
,B=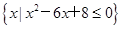 ,则A∩∁RB等于________.
,则A∩∁RB等于________.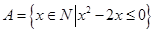 ,则满足
,则满足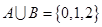 的集合B的个数为( )
的集合B的个数为( )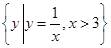 ,则∁UP=( ).
,则∁UP=( ).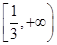
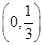
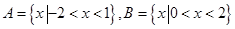 , 则集合
, 则集合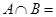 ( )
( )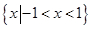
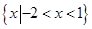
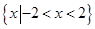
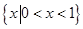
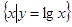 ,B=
,B=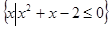 ,则
,则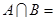 ( )
( )