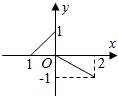
题目内容
12.计算:$\frac{tan7.5°}{1-ta{n}^{2}7.5°}$=$\frac{2-\sqrt{3}}{2}$.分析 利用二倍角的正切函数求解即可.
解答 解:$\frac{tan7.5°}{1-ta{n}^{2}7.5°}$=$\frac{1}{2}×\frac{2tan7.5°}{1-ta{n}^{2}7.5°}$=$\frac{1}{2}$×tan15°=$\frac{1}{2}$×$\frac{sin30°}{1+cos30°}$=$\frac{1}{2}$×$\frac{\frac{1}{2}}{1+\frac{\sqrt{3}}{2}}$=$\frac{2-\sqrt{3}}{2}$.
故答案为:$\frac{2-\sqrt{3}}{2}$.
点评 本题考查二倍角公式的应用,特殊角的三角函数,考查计算能力.

练习册系列答案
相关题目
20.已知集合U={x|x>0},∁UA={x|0<x<2},则集合A=( )
| A. | {x|x≤0或x≥2} | B. | {x|x<0或x>2} | C. | {x|x≥2} | D. | {x|x>2} |
4.已知函数f(x)=asin(πx+α)+bcos(πx+β),且f(2014)=3,则f(2015)的值是( )
| A. | -1 | B. | -2 | C. | -3 | D. | 1 |
9.抛物线y=-$\frac{1}{4}{x}^{2}$的焦点到准线的距离为( )
| A. | 2 | B. | 1 | C. | 4 | D. | 3 |
10.在△ABC中,AC=20,∠A=90°,S△ABC=120,则AB=( )
| A. | 6 | B. | 12 | C. | 24 | D. | 3 |