题目内容
已知函数 既存在极大值又存在极小值,则实数
既存在极大值又存在极小值,则实数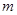 的取值范围是_______________
的取值范围是_______________
 既存在极大值又存在极小值,则实数
既存在极大值又存在极小值,则实数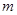 的取值范围是_______________
的取值范围是_______________ 或
或 ;
;本试题主要是考查了一元三次函数的极值问题的运用。
∵函数f(x)=x3+mx2+(m+6)x+1既存在极大值,又存在极小值,f′(x)=3x2+2mx+m+6=0,它有两个不相等的实根,,∴△=4m2-12(m+6)>0,解得m<-3或m>6,故答案为:m<-3或m>6。
解决该试题的关键是三次函数存在两个极值,则说明导函数存在两个零点,其判别式大于零。
∵函数f(x)=x3+mx2+(m+6)x+1既存在极大值,又存在极小值,f′(x)=3x2+2mx+m+6=0,它有两个不相等的实根,,∴△=4m2-12(m+6)>0,解得m<-3或m>6,故答案为:m<-3或m>6。
解决该试题的关键是三次函数存在两个极值,则说明导函数存在两个零点,其判别式大于零。

练习册系列答案
相关题目
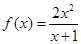 ,
,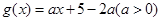 .
.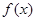 在
在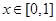 上的值域;
上的值域;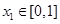 ,总存在
,总存在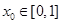 ,使得
,使得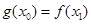 成立,求
成立,求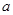 的取值范围.
的取值范围. (a是常数)在[-2,2]上有最大值3,那么在[-2,2]上f(x)的最小值是____________.
(a是常数)在[-2,2]上有最大值3,那么在[-2,2]上f(x)的最小值是____________.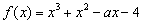 在区间
在区间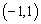 恰有一个极值点,则实数
恰有一个极值点,则实数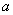 的取值范围为 。
的取值范围为 。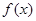 的定义域为
的定义域为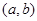 ,其导函数
,其导函数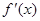 在
在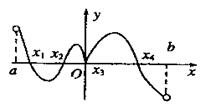
 是
是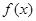 的导函数,
的导函数,
 在
在 处取得极值.
处取得极值. 与
与 满足的关系式;
满足的关系式; ,求函数
,求函数 的单调区间;
的单调区间; ,若存在
,若存在 ,
, ,使得
,使得
 有两个极值点
有两个极值点 、
、 ,且
,且 在区间(0,1)上有极大值,无极小值,则
在区间(0,1)上有极大值,无极小值,则 的取值范围是( )
的取值范围是( ) 



 在
在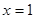 时有极值
时有极值 ,那么
,那么 的值分别为________.
的值分别为________.