ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋÄģļßÐĢΊÔöžÓÓĶ―ėąÏŌĩÉúūÍŌĩŧúŧáĢŽÃŋÄęļųūÝÓĶ―ėąÏŌĩÉúĩÄŨÛšÏËØÖĘšÍŅ§ŌĩģÉžĻķÔŅ§Éú―øÐÐŨÛšÏÆĀđĀĢŽŌŅÖŠÄģÄęķČēÎÓëÆĀđĀĩÄąÏŌĩÉúđēÓÐ2000ÃûĢŪÆäÆĀđĀģÉžĻ![]() ―üËÆĩÄ·þīÓÕýĖŽ·Öēž
―üËÆĩÄ·þīÓÕýĖŽ·Öēž![]() ĢŪÏÖËæŧúģéČĄÁË100ÃûąÏŌĩÉúĩÄÆĀđĀģÉžĻŨũΊŅųąūĢŽēĒ°ŅŅųąūĘýūÝ―øÐÐÁË·ÖŨéĢŽŧæÖÆÁËČįÏÂÆĩÂĘ·ÖēžÖą·―ÍžĢš
ĢŪÏÖËæŧúģéČĄÁË100ÃûąÏŌĩÉúĩÄÆĀđĀģÉžĻŨũΊŅųąūĢŽēĒ°ŅŅųąūĘýūÝ―øÐÐÁË·ÖŨéĢŽŧæÖÆÁËČįÏÂÆĩÂĘ·ÖēžÖą·―ÍžĢš
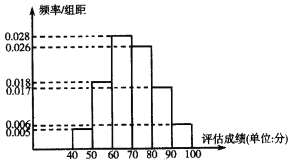
ĢĻ1ĢĐĮóŅųąūÆ―ūųĘý![]() šÍŅųąū·―ēî
šÍŅųąū·―ēî![]() ĢĻÍŽŌŧŨéÖÐĩÄĘýūÝÓÃļÃŨéĮøžäĩÄÖÐĩãÖĩŨũīúąíĢĐĢŧ
ĢĻÍŽŌŧŨéÖÐĩÄĘýūÝÓÃļÃŨéĮøžäĩÄÖÐĩãÖĩŨũīúąíĢĐĢŧ
ĢĻ2ĢĐČôŅ§ÐĢđæķĻÆĀđĀģÉžĻģŽđý82.7·ÖĩÄąÏŌĩÉúŋÉēΞÓ![]() ČýžŌđŦËūĩÄÃæĘÔĢŪ
ČýžŌđŦËūĩÄÃæĘÔĢŪ
ÓÃŅųąūÆ―ūųĘý![]() ŨũΊĩÄđĀžÆÖĩ
ŨũΊĩÄđĀžÆÖĩ![]() ĢŽÓÃŅųąūąęŨžēî
ĢŽÓÃŅųąūąęŨžēî![]() ŨũΊ
ŨũΊ![]() ĩÄđĀžÆÖĩ
ĩÄđĀžÆÖĩ![]() ĢŪĮëĀûÓÃđĀžÆÖĩÅÐķÏÕâ2000ÃûąÏŌĩÉúÖÐĢŽÄÜđŧēΞÓČýžŌđŦËūÃæĘÔĩÄČËĘýĢŧ
ĢŪĮëĀûÓÃđĀžÆÖĩÅÐķÏÕâ2000ÃûąÏŌĩÉúÖÐĢŽÄÜđŧēΞÓČýžŌđŦËūÃæĘÔĩÄČËĘýĢŧ
ļ―Ģš![]() ČôËæŧúąäÁŋ
ČôËæŧúąäÁŋ![]() ĢŽÔō
ĢŽÔō![]() ĢŽ
ĢŽ![]() ĢŪ
ĢŪ
Ąūīð°ļĄŋĢĻ1ĢĐ70ĢŽ161ĢŧĢĻ2ĢĐ317.
Ąū―âÎöĄŋ
ĢĻ1ĢĐļųūÝÆĩÂĘ·ÖēžÖą·―ÍžĢŽ―ášÏÆ―ūųĘýšÍ·―ēîĩÄžÆËãđŦĘ―žīŋÉČÝŌŨĮóĩÃĢŧ
ĢĻ2ĢĐĀûÓÃÕýĖŽ·ÖēžĩÄļÅÂĘĮó―âĢŽĮóĩÃ![]() ĢŽÔŲģËŌÔ
ĢŽÔŲģËŌÔ![]() ĢŽžīŋÉČÝŌŨĮóĩÃ.
ĢŽžīŋÉČÝŌŨĮóĩÃ.
ĢĻ1ĢĐÓÉËųĩÃĘýūÝŧæÖÆĩÄÆĩÂĘÖą·―ÍžĢŽĩÃĢš
ŅųąūÆ―ūųĘý![]() Ģŧ
Ģŧ
Ņųąū·―ēî![]()
![]() Ģŧ
Ģŧ
ĢĻ2ĢĐÓÉĢĻ1ĢĐŋÉÖŠĢŽ![]() ĢŽ
ĢŽ![]() ĢŽđĘÆĀđĀģÉžĻ
ĢŽđĘÆĀđĀģÉžĻ![]() ·þīÓÕýĖŽ·Öēž
·þīÓÕýĖŽ·Öēž![]() ĢŽ
ĢŽ
ËųŌÔ![]() ĢŪ
ĢŪ
ÔÚÕâ2000ÃûąÏŌĩÉúÖÐĢŽÄÜēΞÓČýžŌđŦËūÃæĘÔĩÄđĀžÆÓÐ![]() ČËĢŪ
ČËĢŪ

ĄūĖâÄŋĄŋÐÂÐÍđÚŨīēĄķū·ÎŅŨ![]() ŌßĮé·ĒÉúŌÔĀīĢŽÔÚĘĀ―įļũĩØÖð―ĨÂûŅÓ.ÔÚČŦđúČËÃņĩÄđēÍŽÅŽÁĶšÍļũžķēŋÃÅĩÄŅÏļņđÜŋØÏÂĢŽÎŌđúĩÄŌßĮéŌŅūĩÃĩ―Á˚ܚÃĩÄŋØÖÆ.ČŧķøĢŽÐĄÍõÍŽŅ§·ĒÏÖĢŽÃŋļöđúžŌÔÚŌßĮé·ĒÉúĩÄģõÆÚĢŽÓÉÓÚČÏĘķēŧŨãšÍīëĘĐēŧĩ―ÎŧĢŽļÐČūČËĘýķžŧáģöÏÖŋėËŲĩÄÔöģĪ.ÏÂąíĘĮÐĄÍõÍŽŅ§žĮžĩÄÄģđúÁŽÐø8ĖėÃŋČÕÐÂÐÍđÚŨīēĄķūļÐČūČ·ÕïĩÄĀÛžÆČËĘý.
ŌßĮé·ĒÉúŌÔĀīĢŽÔÚĘĀ―įļũĩØÖð―ĨÂûŅÓ.ÔÚČŦđúČËÃņĩÄđēÍŽÅŽÁĶšÍļũžķēŋÃÅĩÄŅÏļņđÜŋØÏÂĢŽÎŌđúĩÄŌßĮéŌŅūĩÃĩ―Á˚ܚÃĩÄŋØÖÆ.ČŧķøĢŽÐĄÍõÍŽŅ§·ĒÏÖĢŽÃŋļöđúžŌÔÚŌßĮé·ĒÉúĩÄģõÆÚĢŽÓÉÓÚČÏĘķēŧŨãšÍīëĘĐēŧĩ―ÎŧĢŽļÐČūČËĘýķžŧáģöÏÖŋėËŲĩÄÔöģĪ.ÏÂąíĘĮÐĄÍõÍŽŅ§žĮžĩÄÄģđúÁŽÐø8ĖėÃŋČÕÐÂÐÍđÚŨīēĄķūļÐČūČ·ÕïĩÄĀÛžÆČËĘý.
ČÕÆÚīúÂë | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
ĀÛžÆČ·ÕïČËĘý | 4 | 8 | 16 | 31 | 51 | 71 | 97 | 122 |
ΊÁË·ÖÎöļÃđúĀÛžÆļÐČūČËĘýĩÄąäŧŊĮũĘÆĢŽÐĄÍõÍŽŅ§·ÖąðÓÃÁ―ÖÖÄĢÐÍĢšĒŲ![]() ĢŽĒÚ
ĢŽĒÚ![]() ķÔąäÁŋ
ķÔąäÁŋ![]() šÍ
šÍ![]() ĩÄđØÏĩ―øÐÐÄâšÏĢŽĩÃĩ―ÏāÓĶĩÄŧØđé·―ģĖēĒ―øÐÐēÐēî·ÖÎöĢŽēÐēîÍžČįÏÂĢĻŨĒĢšēÐēî
ĩÄđØÏĩ―øÐÐÄâšÏĢŽĩÃĩ―ÏāÓĶĩÄŧØđé·―ģĖēĒ―øÐÐēÐēî·ÖÎöĢŽēÐēîÍžČįÏÂĢĻŨĒĢšēÐēî![]() ĢĐĢšūđýžÆËãĩÃ
ĢĐĢšūđýžÆËãĩÃ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽÆäÖÐ
ĢŽÆäÖÐ![]() ĢŽ
ĢŽ![]() .
.
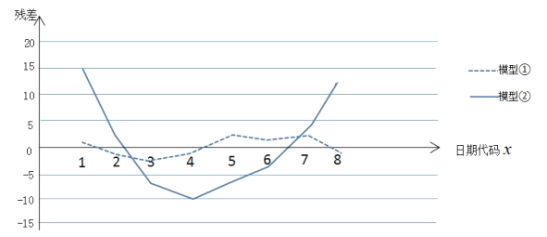
ĢĻ1ĢĐļųūÝēÐēîÍžĢŽąČ―ÏÄĢÐÍĒŲĢŽĒÚĩÄÄâšÏЧđûĢŽÓĶļÃŅĄÔņÄÄļöÄĢÐÍĢŋēĒžōŌŠËĩÃũĀíÓÉĢŧ
ĢĻ2ĢĐļųūÝĢĻ1ĢĐÎĘŅĄķĻĩÄÄĢÐÍĮóģöÏāÓĶĩÄŧØđé·―ģĖĢĻÏĩĘýūųąĢÁôŌŧÎŧÐĄĘýĢĐĢŧ
ĢĻ3ĢĐÓÉÓÚĘąēîĢŽļÃđú―ØÖđĩÚ9ĖėÐÂÐÍđÚŨīēĄķūļÐČūČ·ÕïĩÄĀÛžÆČËĘýÉÐÎīđŦēž.ÐĄÍõÍŽŅ§ČÏΊĢŽČįđû·ĀŌßÐÎĘÆÃŧÓÐĩÃĩ―ÃũÏÔļÄÉÆĢŽÔÚĘýūÝđŦēžÖŪĮ°ŋÉŌÔļųūÝËûÔÚĢĻ2ĢĐÎĘĮóģöĩÄŧØđé·―ģĖĀīķÔļÐČūČËĘýŨũģöÔĪēâĢŽÄĮÃīđĀžÆļÃĩØĮøĩÚ9ĖėÐÂÐÍđÚŨīēĄķūļÐČūČ·ÕïĩÄĀÛžÆČËĘýĘĮķāÉŲ.
ļ―ĢšŧØđéÖąÏßĩÄÐąÂĘšÍ―ØūāĩÄŨîÐĄķþģËđĀžÆđŦĘ―·ÖąðΊĢš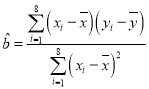 ĢŽ
ĢŽ![]() .
.