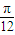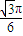题目内容
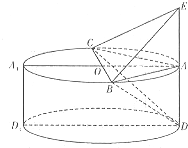 如图,一个几何体由圆柱ADD1A1和三棱锥E-ABC组合而成,点A,B,C在⊙O的圆周上,E,A,D三点共线,已知AB⊥AC,AB=AC,AE=AD=1,BC=2.
如图,一个几何体由圆柱ADD1A1和三棱锥E-ABC组合而成,点A,B,C在⊙O的圆周上,E,A,D三点共线,已知AB⊥AC,AB=AC,AE=AD=1,BC=2.(1)求证:AC⊥BD;
(2)求三棱锥C-BDE的体积.
分析:(1)由已知中EA⊥平面ABC,由线面垂直的性质可得ED⊥AC,结合AC⊥AB,由线面垂直的判定定理可得AC⊥平面EBD,再由线面垂直的性质得到AC⊥BD;
(2)由VC-BDE=VE-ABC+VD-ABC,计算出底面ABC的面积,代入棱锥体积公式,可得答案.
(2)由VC-BDE=VE-ABC+VD-ABC,计算出底面ABC的面积,代入棱锥体积公式,可得答案.
解答:证明:(1)因为EA⊥平面ABC,AC?平面ABC,所以EA⊥AC,即ED⊥AC.
又因为AC⊥AB,AB∩ED=A,所以AC⊥平面EBD.
因为BD?平面EBD,所以AC⊥BD.(4分)
解:(2)VC-BDE=VE-ABC+VD-ABC
又∵S△ABC=
×2×1=1
∴VE-ABC=
×S△ABC×VA=
VD-ABC=
×S△ABC×DA=
∴VC-BDE=
又因为AC⊥AB,AB∩ED=A,所以AC⊥平面EBD.
因为BD?平面EBD,所以AC⊥BD.(4分)
解:(2)VC-BDE=VE-ABC+VD-ABC
又∵S△ABC=
| 1 |
| 2 |
∴VE-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
VD-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
∴VC-BDE=
| 2 |
| 3 |
点评:本题考查的知识点是直线与平面垂直的性质,棱锥的体积,其中熟练掌握空间线面垂直的判定及性质是解答的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 已知一个几何体是由上下两部分构成的组合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为
已知一个几何体是由上下两部分构成的组合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为| 5 |
A、
| ||
B、
| ||
| C、2π | ||
| D、4π |
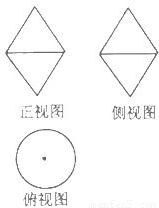
 (2013•泰安二模)如图,一个由两个圆锥组合而成的空间几何体的正视图和侧视图都是边长为1、一个内角为60°的菱形,俯视图是圆及其圆心,那么这个几何体的体积为( )
(2013•泰安二模)如图,一个由两个圆锥组合而成的空间几何体的正视图和侧视图都是边长为1、一个内角为60°的菱形,俯视图是圆及其圆心,那么这个几何体的体积为( )