题目内容
设曲线y=(x-2)2(0<x<2)上动点P处的切线与x轴、y轴分别交于A,B两点,则△AOB面积的最大值为______.
设切点P(x0,y0),(0<x0<2).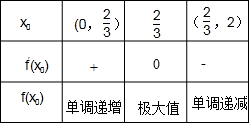
∵y′=2(x-2),∴切线的斜率为2(x0-2).
切线方程为y-(x0-2)2=2(x0-2)(x-x0).
令y=0,解得x=
.∴A(
,0).
令x=0,解得y=4-
.∴B(0,4-
).
∴S△AOB=
|AO||OB|=
×
×|4-
|=
(-
-2
+4x0+8).
令f(x0)=-
-2
+4x0+8,则f′(x0)=-3
-4x0+4=-(3x0-2)(x0+2).
令f′(x0)=0,又0<x0<2,解得x0=
.列表如下:
由表格可得到:当x=
时,f(x0)取得极大值,也即最大值.
此时,S△AOB取得最大值,
[-(
)3-2(
)2+4×(
)+8]=
.
故答案为
.

∵y′=2(x-2),∴切线的斜率为2(x0-2).
切线方程为y-(x0-2)2=2(x0-2)(x-x0).
令y=0,解得x=
| x0+2 |
| 2 |
| x0+2 |
| 2 |
令x=0,解得y=4-
| x | 20 |
| x | 20 |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| |x0+2| |
| 2 |
| x | 20 |
| 1 |
| 4 |
| x | 30 |
| x | 20 |
令f(x0)=-
| x | 30 |
| x | 20 |
| x | 20 |
令f′(x0)=0,又0<x0<2,解得x0=
| 2 |
| 3 |
由表格可得到:当x=
| 2 |
| 3 |
此时,S△AOB取得最大值,
| 1 |
| 4 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 64 |
| 27 |
故答案为
| 64 |
| 27 |

练习册系列答案
相关题目

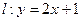 求:
求: 关于
关于 的对称的直线方程。
的对称的直线方程。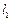 :
: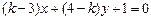 与直线
与直线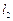 :
: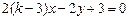 平行,则
平行,则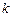 的值等于( )
的值等于( ) y+a=0(a为实常数)的倾斜角的大小是____________.
y+a=0(a为实常数)的倾斜角的大小是____________.