题目内容
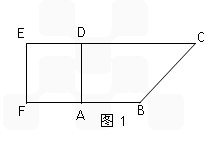
如图(1)在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=| 1 | 2 |
(1)求证:PA∥平面EFG;
(2)求二面角E-FG-D的余弦值的绝对值.
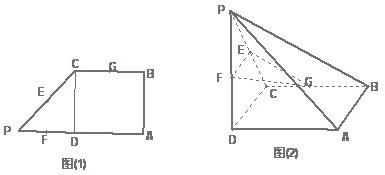
分析:(1)要证PA∥平面EFG,可以证明PA所在平面与平面FEG平行即可.
(2)求二面角E-FG-D的余弦值的绝对值.建立空间直角坐标系,利用法向量的数量积求解即可.
(2)求二面角E-FG-D的余弦值的绝对值.建立空间直角坐标系,利用法向量的数量积求解即可.
解答: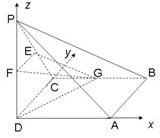 解:由题意,将△PCD沿CD折起后,PA⊥平面ABCD.四边形ABCD是边长为2的正方形,PD=2.
解:由题意,将△PCD沿CD折起后,PA⊥平面ABCD.四边形ABCD是边长为2的正方形,PD=2.
(1)因为点E,F,G分别是PC,PD,BC的中点,
所以EF∥CD,EG∥PB.
又因为CD∥AB,所以EF∥AB,因为AB?平面EFG,
EF?平面EFG,所以AB∥平面EFG,
同理PBAB∥平面EFG,又因为PB∩AB=B,
所以平面EFG∥平面PAB,PA?平面PAB,
所以PA∥平面EFG.
(2)建立空间直角坐标系D-xyz,如图,
则D(0,0,0),F(0,0,1),G(1,2,0),E(0,1,1),
=(0,0,1),
=(1,2,0),
=(0,-1,0),
=(1,1,-1).
求出平面DFG的法向量m=(-2,1,0),
平面EFG的法向量,n=(1,0,1).
所以|cos?m,n?|=
=
.
 解:由题意,将△PCD沿CD折起后,PA⊥平面ABCD.四边形ABCD是边长为2的正方形,PD=2.
解:由题意,将△PCD沿CD折起后,PA⊥平面ABCD.四边形ABCD是边长为2的正方形,PD=2.(1)因为点E,F,G分别是PC,PD,BC的中点,
所以EF∥CD,EG∥PB.
又因为CD∥AB,所以EF∥AB,因为AB?平面EFG,
EF?平面EFG,所以AB∥平面EFG,
同理PBAB∥平面EFG,又因为PB∩AB=B,
所以平面EFG∥平面PAB,PA?平面PAB,
所以PA∥平面EFG.
(2)建立空间直角坐标系D-xyz,如图,
则D(0,0,0),F(0,0,1),G(1,2,0),E(0,1,1),
| DF |
| DG |
| EF |
| EG |
求出平面DFG的法向量m=(-2,1,0),
平面EFG的法向量,n=(1,0,1).
所以|cos?m,n?|=
| |m•n| |
| |m||n| |
| ||
| 5 |
点评:本题考查空间平面与平面之间的位置关系,空间直角坐标系,法向量,数量积等知识,是难题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
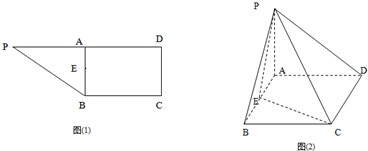
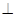 AD且AB=AD=
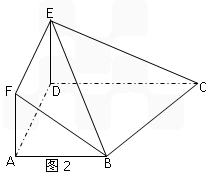
AD且AB=AD=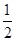 CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
 中,
中,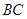 ∥
∥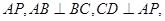
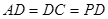 =2,
=2,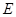 、
、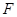 、
、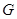 分别是
分别是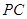 、
、 、
、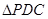 沿
沿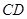 折起,使平面
折起,使平面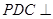 平面
平面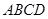 (如图2).
(如图2). 的大小;
的大小;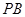 上确定一点
上确定一点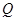 ,使
,使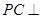 平面
平面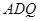 ,并给出证明过程.
,并给出证明过程.
 CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。