题目内容
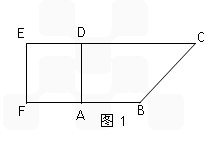
如图(1)在直角梯形ABCD中,AB//CD,AB AD且AB=AD=
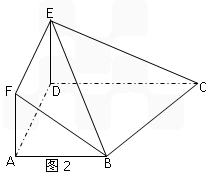
AD且AB=AD=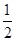 CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。

(1)求证平面BDE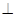 平面BEC
平面BEC
(2)求直线BD与平面BEF所成角的正弦值。
【答案】
⑴证见解析 ⑵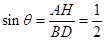
【解析】(1)由折前折后线面的位置关系得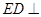 平面
平面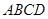 ,所以
,所以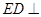
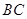 ,又在
,又在 中,
中,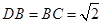 ,
,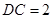 ,三边满足勾股定理,
,三边满足勾股定理,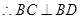 。由线面垂直的判定定理即证得结论。
。由线面垂直的判定定理即证得结论。
(2)因为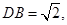 只需求出点
只需求出点 到平面
到平面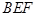 的距离也是点
的距离也是点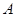 到平面
到平面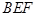 的距离,易证出
的距离,易证出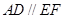 ,
, 平面
平面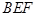 ,由面面垂直的判定定理得平面
,由面面垂直的判定定理得平面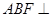 平面
平面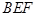 ,
,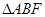 中
中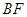 边上的高就是点
边上的高就是点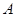 到平面
到平面 的距离。根据线面角的定义可求直线BD与平面BEF所成角的正弦值。
的距离。根据线面角的定义可求直线BD与平面BEF所成角的正弦值。

练习册系列答案
相关题目
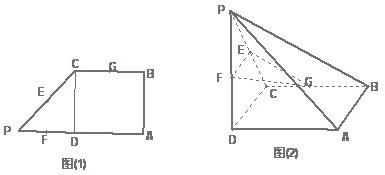
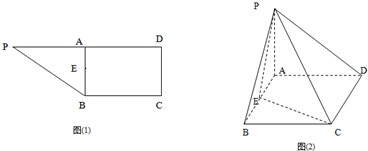
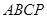 中,
中,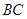 ∥
∥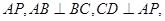
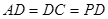 =2,
=2,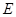 、
、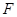 、
、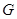 分别是
分别是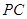 、
、 、
、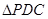 沿
沿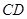 折起,使平面
折起,使平面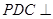 平面
平面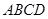 (如图2).
(如图2). 的大小;
的大小;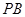 上确定一点
上确定一点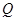 ,使
,使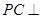 平面
平面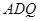 ,并给出证明过程.
,并给出证明过程.
 CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。