题目内容
(14分)已知函数![]() ,点
,点![]() ,点
,点![]() ,
,
(1)若![]() ,求函数
,求函数![]() 的单调递增区间;(2)若
的单调递增区间;(2)若![]() ,函数
,函数![]() 在
在![]() 处取得极值,且
处取得极值,且![]() ,求证:向量
,求证:向量![]() 与向量
与向量![]() 不可能垂直;(3)若函数
不可能垂直;(3)若函数![]() 的导函数
的导函数![]() 满足:当
满足:当![]() 时,有
时,有![]() 恒成立,求函数的解析式。
恒成立,求函数的解析式。
(Ⅰ) ![]() (Ⅱ) 略 (Ⅲ)
(Ⅱ) 略 (Ⅲ)![]()
解析:
(1)当![]() 时,
时,![]()
由![]() 可得
可得![]() ,则函数的单调递增区间是
,则函数的单调递增区间是![]() 。(3分)
。(3分)
(2)![]() 函数
函数![]() 在
在![]() 处取得极值,
处取得极值,![]()
![]() 即
即![]() 是方程
是方程![]() 两根,
两根,
![]() 。 (5分)
。 (5分)
设![]() ,则
,则![]() 即:
即:![]()
![]() (6分)
(6分)
![]()
![]() 代入化简得:
代入化简得:![]()
已知![]() 即
即![]() ,矛盾,则向量
,矛盾,则向量![]() 与向量
与向量![]() 不可能垂直。(8分)
不可能垂直。(8分)
(3)函数![]() 的导函数
的导函数![]() 满足:
满足:
当![]() 时,有
时,有![]() 恒成立,
恒成立,
则![]()
![]()
![]() , ∴ab=
, ∴ab=![]() (11分)
(11分)
![]()
所以二次函数![]() 的对称轴
的对称轴![]()
![]() ,即
,即![]() ,则:
,则:![]() ,
,
![]() 。 (14
。 (14

练习册系列答案
相关题目
 已知函数y=f(x)的导函数y=f′(x)的图象如图,则( )
已知函数y=f(x)的导函数y=f′(x)的图象如图,则( ) 的定义域为
的定义域为 ,部分对应值如下表,
,部分对应值如下表, 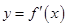 的图象如图所示.下列关于
的图象如图所示.下列关于

 ,
, ;
; 上是减函数;
上是减函数; 时,
时, 的最大值为4;
的最大值为4; 时,函数
时,函数 有
有 的图像与函数
的图像与函数 的图像关于直线
的图像关于直线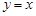 对称,那么下列情形不可能出现的是( )
对称,那么下列情形不可能出现的是( )