题目内容
2008年10月10日至15日,孝感市第三届运动会胜利召开.在安全保障方面,警方从警犬训练基地挑选防暴犬时,从体能、嗅觉、反应三项指标进行检测,如果这三项中至少有两项通过即可入选.假定某基地有4只警犬(分别记为A、B、C、D)拟参加挑选,且每只犬能通过体能、嗅觉、反应的概率分别为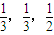 ,这三项测试能否通过相互之间没有影响.
,这三项测试能否通过相互之间没有影响.(1)求犬A能够入选的概率;
(2)规定:每有一只防暴犬入选,则相应的训练基地积3分,否则积0分.求该基地总积分的期望.
【答案】分析:(1)将事件:“犬A能够入选”分解为四个事件的和,再分别用相互独立事件的概率乘法公式算出相应的概率,最后用概率的加法公式将所得概率相加,就得到犬A能够入选的概率;
(2)解法一:先通过基本事件可以数出变量ξ的取值有五种:0,3,6,9,12,再分别求出这五个变量值对应的概率,列出离散型随机变量的分布表格,最后根据这个二维表格可以算出基地总积分的期望值.
解法二:因为该基地总积分为ξ,ξ服从二项分布: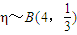 ,利用二项分布的公式可以求出E(η)=
,利用二项分布的公式可以求出E(η)= ,最后可以算出Eξ=E(3η)=4.
,最后可以算出Eξ=E(3η)=4.
解答:解:(1)记警犬A能够入选为事件A,则
P(A)=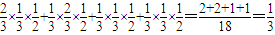 -------(5分)
-------(5分)
(2)解法一:记该基地总积分为ξ,则ξ的所有可能取值为:0,3,6,9,12.------(6分)
且 ;
;
 ;
;
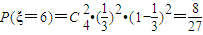 ;
;
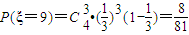 ;
;
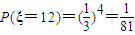
∴ξ的分布列为------------------------------(10分)
故期望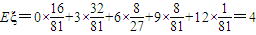 ------------------------------12
------------------------------12
解法二:记该基地总积分为ξ,η只防爆犬入选,则η的所有可能值为0,1,2,3,4(6分)
因而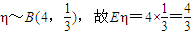 .(10分)
.(10分)
又ξ=3η
∴Eξ=E(3η)=3Eη=4.(12分)
答:(I)犬A能够入选的概率为 ;(II)该基地总积分的期望为4.
;(II)该基地总积分的期望为4.
点评:本题考查了离散型随机变量的期望与方差的算法,属于中档题.读懂题中的概率,准确运用概率的乘法公式和加法公式算出相应变量值的概率,利用随机变量的二维表格进行计算,是解决本题的关键.
(2)解法一:先通过基本事件可以数出变量ξ的取值有五种:0,3,6,9,12,再分别求出这五个变量值对应的概率,列出离散型随机变量的分布表格,最后根据这个二维表格可以算出基地总积分的期望值.
解法二:因为该基地总积分为ξ,ξ服从二项分布:
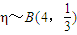 ,利用二项分布的公式可以求出E(η)=
,利用二项分布的公式可以求出E(η)= ,最后可以算出Eξ=E(3η)=4.
,最后可以算出Eξ=E(3η)=4.解答:解:(1)记警犬A能够入选为事件A,则
P(A)=
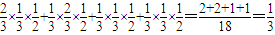 -------(5分)
-------(5分)(2)解法一:记该基地总积分为ξ,则ξ的所有可能取值为:0,3,6,9,12.------(6分)
且
 ;
;  ;
;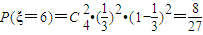 ;
;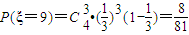 ;
;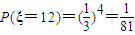
| ξ | 3 | 6 | 9 | 12 | |
| P | 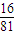 | 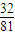 | 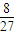 | 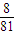 | 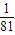 |
故期望
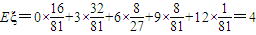 ------------------------------12
------------------------------12解法二:记该基地总积分为ξ,η只防爆犬入选,则η的所有可能值为0,1,2,3,4(6分)
因而
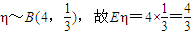 .(10分)
.(10分)又ξ=3η
∴Eξ=E(3η)=3Eη=4.(12分)
答:(I)犬A能够入选的概率为
 ;(II)该基地总积分的期望为4.
;(II)该基地总积分的期望为4.点评:本题考查了离散型随机变量的期望与方差的算法,属于中档题.读懂题中的概率,准确运用概率的乘法公式和加法公式算出相应变量值的概率,利用随机变量的二维表格进行计算,是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
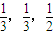 ,这三项测试能否通过相互之间没有影响.
,这三项测试能否通过相互之间没有影响.