题目内容
17.在平面直角坐标系中,已知A($\sqrt{3}$,0),B(0,1),C($\sqrt{3}$,1),则以下命题:①若点P是△ABC的三边垂直平分线的交点,则$\overrightarrow{PA}$+$\overrightarrow{PB}$=$\overrightarrow{0}$;
②若点P是△ABC的三条中线的交点,则$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{0}$;
③若点P是△ABC三条内角平分线的交点,则$\sqrt{3}\overrightarrow{PA}+\overrightarrow{PB}+2\overrightarrow{PC}$=$\overrightarrow{0}$.
正确的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①先根据A,B,C三点坐标可知△ABC为Rt△,BC⊥AC,画出图形便可看出P为AB中点,从而$\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{0}$正确;
②根据向量加法的平行四边形法则及重心的性质便可判断该命题正确;
③该命题中,P为△ABC的三条内角平分线交点,而根据A,B,C的坐标便可得出∠BAC=60°,从而可以求出直线PC和PA的倾斜角,从而可以写出这两直线的方程,联立方程便可解出P点的坐标,然后便可得到向量$\overrightarrow{PA},\overrightarrow{PB},\overrightarrow{PC}$的坐标,从而可以求出$\sqrt{3}\overrightarrow{PA}+\overrightarrow{PB}+2\overrightarrow{PC}$的坐标,便可判断该命题的正误.
解答 解:①如图,根据A,B,C三点的坐标便知AC⊥BC,△ABC是直角三角形;
P点是△ABC三边垂直平分线的交点;
∴P点为边AB的中点;
∴$\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{0}$;
②如图,P为△ABC三条中线的交点,设AB中点为D,则$\overrightarrow{PA}+\overrightarrow{PB}=2\overrightarrow{PD}=\overrightarrow{CP}$;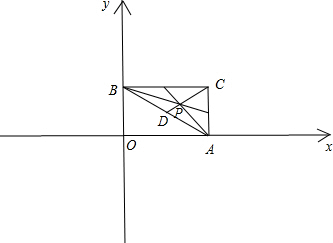 ∴$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{0}$;
∴$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{0}$;
③如图,P是△ABC三条内角平分线的交点,根据A,B,C三点坐标知:∠BAC=60°;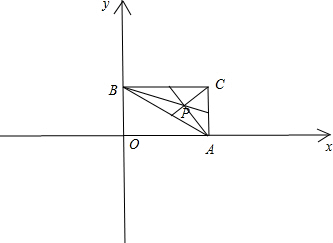 ∴直线PA的倾斜角为120°,PC的倾斜角为45°;
∴直线PA的倾斜角为120°,PC的倾斜角为45°;
∴直线PA的方程为:$y=-\sqrt{3}(x-\sqrt{3})$,直线PC的方程为:$y-1=x-\sqrt{3}$;
∴联立这两个方程组解得$\left\{\begin{array}{l}{x=\frac{\sqrt{3}+1}{2}}\\{y=\frac{3-\sqrt{3}}{2}}\end{array}\right.$;
∴$\overrightarrow{PA}=(\frac{\sqrt{3}-1}{2},\frac{\sqrt{3}-3}{2})$,$\overrightarrow{PB}=(-\frac{\sqrt{3}+1}{2},\frac{\sqrt{3}-1}{2})$,$\overrightarrow{PC}=(\frac{\sqrt{3}-1}{2},\frac{\sqrt{3}-1}{2})$;
∴$\sqrt{3}\overrightarrow{PA}+\overrightarrow{PB}+2\overrightarrow{PC}$=$(\frac{3-\sqrt{3}}{2},\frac{3-3\sqrt{3}}{2})+(-\frac{\sqrt{3}+1}{2},\frac{\sqrt{3}-1}{2})$$+(\sqrt{3}-1,\sqrt{3}-1)$=(0,0)=$\overrightarrow{0}$;
∴这三个命题都正确.
故选:D.
点评 考查三角形中位线的性质,相反向量的概念,三角形重心的概念,重心的性质:到顶点距离是它到对边中点距离的2倍,向量加法的平行四边形法则,直线倾斜角和斜率的概念,直线的点斜式方程,以及向量坐标的加法和数乘运算.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |