Question

【题目】已知自变量为的函数的极大值点为，，为自然对数的底数.

（1）若，证明：有且仅有2个零点；

（2）若，，，…，为任意正实数，证明：.

Answer 1

【答案】（1）证明见解析；（2）证明见解析

【解析】

（1）当时，，求导得，令，再次求导，可判断在单调递减，又，故在上单调递增；在上单调递减；求得，再判断，，结合零点存在定理判断，有且仅有2个零点；

（2）对求导可得，又，故可判断，；，，在上单调递增；在上单调递减；故且，所求问题转化为，

记为，观察知为等差乘以等比数列的形式，结合错位相减法化简即可求证；

解：（1）由题知：，

∴，令，，

∴在单调递减，又∵，

∴，，，，

故在上单调递增；在上单调递减；所以；

又因为，，

所以在，上各恰有零点，即有且仅有2个零点.

（2）由题知，

因此，，；，，

故在上单调递增；在上单调递减；

因此且，

∵，所以，

记为，所以，

，

所以，

所以，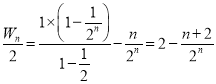

所以，

因此，即.