题目内容
已知函数f(x)=x2+2|lnx-1|.(1)求函数y=f(x)的最小值;
(2)证明:对任意x∈[1,+∞),lnx≥
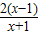 恒成立;
恒成立;(3)对于函数f(x)图象上的不同两点A(x1,y1),B(x2,y2)(x1<x2),如果在函数f(x)图象上存在点M(x,y)(其中x∈(x1,x2))使得点M处的切线l∥AB,则称直线AB存在“伴侣切线”.特别地,当x=
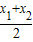 时,又称直线AB存在“中值伴侣切线”.试问:当x≥e时,对于函数f(x)图象上不同两点A、B,直线AB是否存在“中值伴侣切线”?证明你的结论.
时,又称直线AB存在“中值伴侣切线”.试问:当x≥e时,对于函数f(x)图象上不同两点A、B,直线AB是否存在“中值伴侣切线”?证明你的结论.
【答案】分析:(1)对x分类讨论,利用导数研究其单调性、极值与最值即可得出;
(2)构造函数令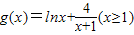 ,利用导数研究其单调性与极值即可得出;
,利用导数研究其单调性与极值即可得出;
(3)利用斜率计算公式和导数的几何意义即可得出关于t=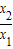 的关系式,再利用(2)的结论即可判断出是否存在.
的关系式,再利用(2)的结论即可判断出是否存在.
解答:解:(1)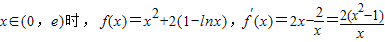 ,
,
令f′(x)>0得x∈(1,e);f′(x)<0得x∈(0,1).
∴f′(x)在(0,1]上单减,在[1,e)上单增;
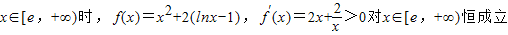 .
.
∴f(x)在[e,+∞)单调递增.
故f(x)min=f(1)=3.
(2)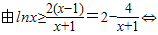
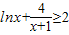
令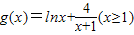 ,
,
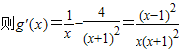 ,
,
因为x≥1,显然g'(x)≥0,所以g(x)在[1,+∞)上递增,
显然有g(x)≥g(1)=2恒成立.(当且仅当x=1时等号成立),即证.
(3)当x≥e时,f(x)=x2+2(lnx-1),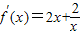 ,假设函数f(x)存在“中值伴侣切线”.
,假设函数f(x)存在“中值伴侣切线”.
设A(x1,y1),B(x2,y2)是曲线y=f(x)上的不同两点,且0<x1<x2,
则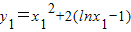 ,
,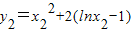 .
.
故直线AB的斜率: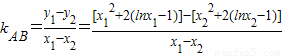 =
=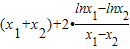 .
.
曲线在点M(x,y)处的切线斜率:
k=f′(x)=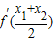 =
=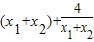 .
.
依题意得: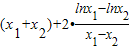 =
=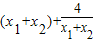
化简可得: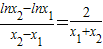 ,即
,即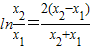 =
=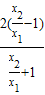 .
.
设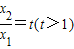 ,上式化为
,上式化为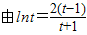 ,由(2)知t>1时,
,由(2)知t>1时,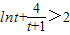 恒成立.
恒成立.
所以在(1,+∞)内不存在t,使得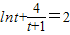 成立.
成立.
综上所述,假设不成立.所以,函数f(x)不存在“中值伴侣切线”.
点评:熟练掌握利用导数研究函数的单调性、极值与最值、导数的几何意义、分类讨论思想方法、斜率的计算公式、问题等价转化等是解题的关键.
(2)构造函数令
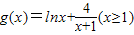 ,利用导数研究其单调性与极值即可得出;
,利用导数研究其单调性与极值即可得出;(3)利用斜率计算公式和导数的几何意义即可得出关于t=
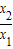 的关系式,再利用(2)的结论即可判断出是否存在.
的关系式,再利用(2)的结论即可判断出是否存在.解答:解:(1)
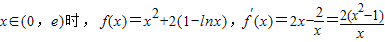 ,
,令f′(x)>0得x∈(1,e);f′(x)<0得x∈(0,1).
∴f′(x)在(0,1]上单减,在[1,e)上单增;
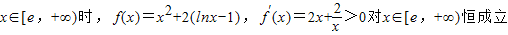 .
.∴f(x)在[e,+∞)单调递增.
故f(x)min=f(1)=3.
(2)
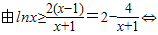
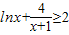
令
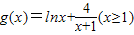 ,
,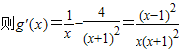 ,
,因为x≥1,显然g'(x)≥0,所以g(x)在[1,+∞)上递增,
显然有g(x)≥g(1)=2恒成立.(当且仅当x=1时等号成立),即证.
(3)当x≥e时,f(x)=x2+2(lnx-1),
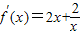 ,假设函数f(x)存在“中值伴侣切线”.
,假设函数f(x)存在“中值伴侣切线”.设A(x1,y1),B(x2,y2)是曲线y=f(x)上的不同两点,且0<x1<x2,
则
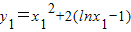 ,
,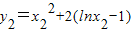 .
.故直线AB的斜率:
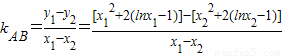 =
=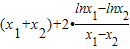 .
.曲线在点M(x,y)处的切线斜率:
k=f′(x)=
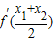 =
=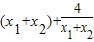 .
.依题意得:
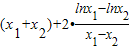 =
=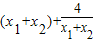
化简可得:
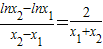 ,即
,即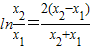 =
=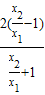 .
.设
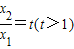 ,上式化为
,上式化为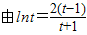 ,由(2)知t>1时,
,由(2)知t>1时,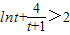 恒成立.
恒成立.所以在(1,+∞)内不存在t,使得
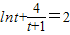 成立.
成立.综上所述,假设不成立.所以,函数f(x)不存在“中值伴侣切线”.
点评:熟练掌握利用导数研究函数的单调性、极值与最值、导数的几何意义、分类讨论思想方法、斜率的计算公式、问题等价转化等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|