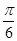题目内容
如图,在直三棱柱ABC—A1B1C1中, 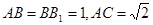 ,直线B1C与平面ABC成45°角。
,直线B1C与平面ABC成45°角。

(1)求证:平面A1B1C⊥平面B1BCC1;
(2)求二面角A—B1C—B的余弦值.
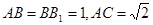 ,直线B1C与平面ABC成45°角。
,直线B1C与平面ABC成45°角。
(1)求证:平面A1B1C⊥平面B1BCC1;
(2)求二面角A—B1C—B的余弦值.
(1)参考解析;(2)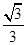
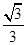
试题分析:(1)要证明平面
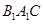 ⊥平面
⊥平面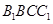 ,从图形中确定证明
,从图形中确定证明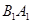 垂直于平面
垂直于平面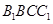 .从而要在平面
.从而要在平面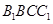 中找到两条相交直线与
中找到两条相交直线与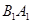 垂直.显然
垂直.显然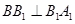 .通过计算可得直线
.通过计算可得直线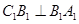 .所以可得直线与平面垂直.
.所以可得直线与平面垂直.(2)要求二面角A—B1C—B的余弦值,要找的这二面角的平面角.通过计算可得
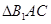 是等边三角形,并且
是等边三角形,并且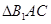 是等腰直角三角形.所以只要取
是等腰直角三角形.所以只要取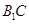 的中点O.即可得角AOB为所求的二面角的平面角.应用余弦定理即可求得.
的中点O.即可得角AOB为所求的二面角的平面角.应用余弦定理即可求得.试题解析:(1)证:∵BB1⊥面ABC
∴B1C与面ABC所成的角为∠B1CB
∴∠B1CB=450
∵BB1=1
∴BC=1
又∵BA=1,AC=
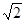
∴AB2+BC2=AC2
∴AB⊥BC
∵BB1⊥AB
BB1∩BC=B
∴AB⊥面B1BCC1
∵A1B1//AB
∴A1B1⊥面B1BCC1.∵A1B1
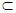 面A1B1C
面A1B1C∴面A1B1C⊥面B1BCC1
(2)因为直角三角形
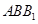 中,
中,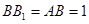 .所以
.所以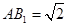 .所以
.所以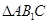 为等边三角形.又因为
为等边三角形.又因为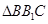 为等腰三角形.所以取
为等腰三角形.所以取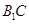 得中点O,连结AO,BO,则
得中点O,连结AO,BO,则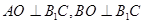 所以
所以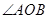 为二面角A-
为二面角A-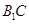 -B的平面角.因为直角三角形
-B的平面角.因为直角三角形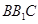 中.
中. 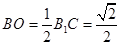 .在等边三角形中.
.在等边三角形中. 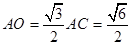 .所以在三角形
.所以在三角形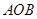 中.
中. 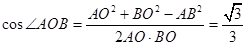

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,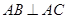 ,
,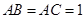 ,
,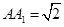 ,D为BC中点.
,D为BC中点.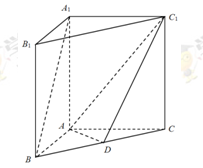
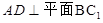 ;
; ;
;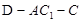 的正弦值.
的正弦值.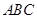 的直角边
的直角边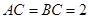 ,沿其中位线
,沿其中位线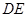 将平面
将平面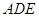 折起,使平面
折起,使平面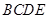 ,得到四棱锥
,得到四棱锥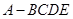 ,设
,设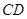 、
、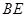 、
、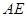 、
、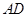 的中点分别为
的中点分别为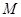 、
、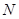 、
、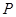 、
、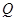 .
.


 平面
平面 ;
; 所成的角.
所成的角.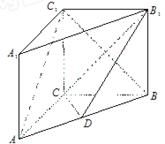
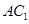 ∥平面
∥平面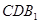 ;
;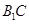 所成角的余弦值.
所成角的余弦值.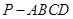 的底面
的底面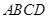 为矩形,且
为矩形,且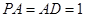 ,
,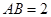 ,
,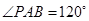 ,
, ,
,
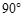 ,且AB=2AD=2DC=2PD=4,E为PA的中点.
,且AB=2AD=2DC=2PD=4,E为PA的中点.
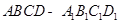 中,
中, ,
, 分别为棱
分别为棱 ,
,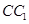 的中点,在平面
的中点,在平面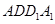 内且与平面
内且与平面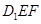 平行的直线( )
平行的直线( ) ,那么平面
,那么平面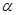 内一定存在直线平行于平面
内一定存在直线平行于平面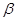 ;
; ,平面
,平面 ,
,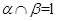 ,那么
,那么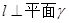 ;
;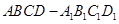 中,
中,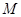 、
、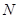 分别是
分别是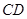 、
、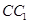 的中点,则异面直线
的中点,则异面直线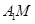 与
与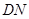 所成角的大小是( )
所成角的大小是( )