题目内容
(2009•枣庄一模)设双曲线mx2+ny2=1的一个焦点与抛物线y=
x2的焦点相同,离心率为2,则此双曲线的渐近线方程为
| 1 |
| 8 |
y=±
x
| ||
| 3 |
y=±
x
.
| ||
| 3 |
分析:利用抛物线的方程先求出抛物线的焦点即双曲线的焦点,利用双曲线的方程与系数的关系求出a2,b2,利用双曲线的三个系数的关系列出m,n的一个关系,再利用双曲线的离心率的公式列出关于m,n的另一个等式,解方程组求出m,n的值,代入方程求出双曲线的方程.
解答:解:∵抛物线x2=8y的焦点为(0,2)
∴mx2+ny2=1的一个焦点为(0,2)
∴焦点在y轴上
∴a2=
,b2=-
,c=2
根据双曲线三个参数的关系得到 4=a2+b2=
-
又离心率为2即
=4
解得n=1,m=-
∴此双曲线的方程为 y2-
=0
即:y=±
x
故答案为:y=±
x
∴mx2+ny2=1的一个焦点为(0,2)
∴焦点在y轴上
∴a2=
| 1 |
| n |
| 1 |
| m |
根据双曲线三个参数的关系得到 4=a2+b2=
| 1 |
| n |
| 1 |
| m |
又离心率为2即
| 4 | ||
|
解得n=1,m=-
| 1 |
| 3 |
∴此双曲线的方程为 y2-
| x2 |
| 3 |
即:y=±
| ||
| 3 |
故答案为:y=±
| ||
| 3 |
点评:解决双曲线、椭圆的三参数有关的问题,有定注意三参数的关系:c2=a2+b2而椭圆中三参数的关系为a2=c2+b2

练习册系列答案
相关题目
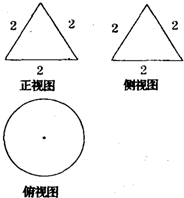 (2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )
(2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )