题目内容
已知等差数列![]() 中,
中,![]() 是其前
是其前![]() 项和,
项和,![]() ,求:
,求:![]() 及
及![]() .
.
![]() =8及
=8及![]()
![]()
解析:
设等差数列![]() 的公差为
的公差为![]() ,则
,则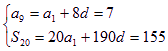
解得,![]() (8分)
(8分)
![]()
![]() ,
,![]() .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
题目内容
已知等差数列![]() 中,
中,![]() 是其前
是其前![]() 项和,
项和,![]() ,求:
,求:![]() 及
及![]() .
.
![]() =8及
=8及![]()
![]()
设等差数列![]() 的公差为
的公差为![]() ,则
,则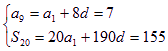
解得,![]() (8分)
(8分)
![]()
![]() ,
,![]() .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案