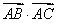Question

如图，直线AB为圆O的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于点D.

(1)证明：DB＝DC；

(2)设圆的半径为1，BC＝，延长CE交AB于点F，求△BCF外接圆的半径．

 

Answer 1

(1)见解析 (2)

【解析】

(1)证明　连接DE，则∠DCB＝∠DEB，

∵DB⊥BE，

∴∠DBC＋∠CBE＝90°，∠DEB＋∠EDB＝90°，

∴∠DBC＋∠CBE＝∠DEB＋∠EDB，

又∠CBE＝∠EBF＝∠EDB，

∴∠DBC＝∠DEB＝∠DCB，

∴DB＝DC.

(2)解　由(1)知：∠CBE＝∠EBF＝∠BCE，

∴∠BDE＝∠CDE，

∴DE是BC的垂直平分线，

设交点为H，则BH＝，

∴OH＝＝，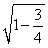

∴DH＝，

∴tan∠BDE＝＝，

∴∠BDE＝30°，

∴∠FBE＝∠BDE＝30°，

∴∠CBF＋∠BCF＝90°，

∴∠BFC＝90°，

∴BC是△BCF的外接圆直径．

∴△BCF的外接圆半径为