题目内容
已知点P是圆x2+y2=1上的一个动点,过点P作PQ⊥x轴于点Q,设
(1)求点M的轨迹方程
(2)求向量
 和
和 夹角的最大值,并求此时P点的坐标.
夹角的最大值,并求此时P点的坐标.
【答案】分析:(1)设P(x°,y°),M(x,y),由条件可得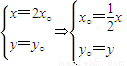 ,再由 x°2+y°2=1,得到
,再由 x°2+y°2=1,得到 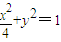 .
.
(2)设向量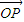 与
与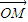 的夹角为α,
的夹角为α,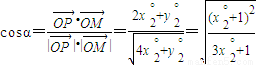 ,令t=3x°2+1,则
,令t=3x°2+1,则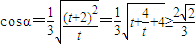 ,由此求得结论.
,由此求得结论.
解答:解:(1)设P(x°,y°),M(x,y),则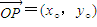 ,
, ,
,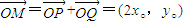 =(x,y).
=(x,y).
∴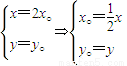 ,∵x°2+y°2=1,∴
,∵x°2+y°2=1,∴ .
.
(2)设向量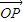 与
与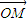 的夹角为α,则
的夹角为α,则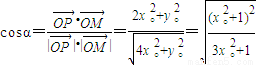
令t=3x°2+1,则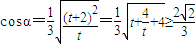 ,
,
当且仅当t=2时,即P点坐标为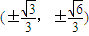 时,等号成立.∴
时,等号成立.∴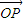 与
与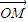 夹角的最大值是
夹角的最大值是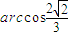 .
.
点评:本题考查点轨迹方程的求法,两个向量坐标形式的运算,两个向量夹角公式和基本不等式的应用,得到
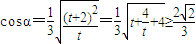 ,是解题的难点.
,是解题的难点.
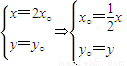 ,再由 x°2+y°2=1,得到
,再由 x°2+y°2=1,得到 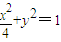 .
.(2)设向量
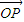 与
与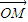 的夹角为α,
的夹角为α,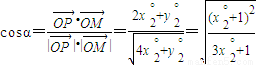 ,令t=3x°2+1,则
,令t=3x°2+1,则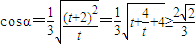 ,由此求得结论.
,由此求得结论.解答:解:(1)设P(x°,y°),M(x,y),则
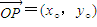 ,
, ,
,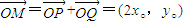 =(x,y).
=(x,y).∴
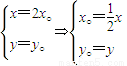 ,∵x°2+y°2=1,∴
,∵x°2+y°2=1,∴ .
.(2)设向量
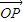 与
与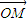 的夹角为α,则
的夹角为α,则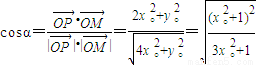
令t=3x°2+1,则
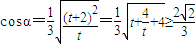 ,
,当且仅当t=2时,即P点坐标为
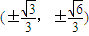 时,等号成立.∴
时,等号成立.∴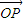 与
与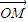 夹角的最大值是
夹角的最大值是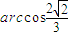 .
.点评:本题考查点轨迹方程的求法,两个向量坐标形式的运算,两个向量夹角公式和基本不等式的应用,得到
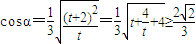 ,是解题的难点.
,是解题的难点. 
练习册系列答案
相关题目
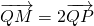 的点M的轨迹为曲线C.
的点M的轨迹为曲线C. 的点M的轨迹为曲线C.
的点M的轨迹为曲线C.