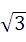题目内容
直线x-y+m=0与圆x2+y2-2x-1=0有两个不同的交点的充要条件为( ).
| A.m<1 | B.-3<m<1 | C.-4<m<2 | D.0<m<1 |
B
解析试题分析:联立直线与圆的方程得: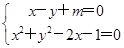 ,消去y得:2x2+(2m-2)x+m2-1=0,由题意得:△=(2m-2)2-8(m2-1)=-4(m+1)2+16>0,变形得:(m+3)(m-1)<0,解得:-3<m<1,故选B.
,消去y得:2x2+(2m-2)x+m2-1=0,由题意得:△=(2m-2)2-8(m2-1)=-4(m+1)2+16>0,变形得:(m+3)(m-1)<0,解得:-3<m<1,故选B.
考点:直线与圆相交的性质;以及充分必要条件的判断.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
若圆C: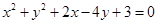 关于直线
关于直线 对称,则由点
对称,则由点 向圆所作的切线长的最小值是( )
向圆所作的切线长的最小值是( )
| A.2 | B.4 | C.3 | D.6 |
若圆的方程为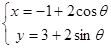 (
( 为参数),直线的方程为
为参数),直线的方程为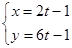 (t为参数),
(t为参数),
则直线与圆的位置关系是( )
| A.相交过圆心 | B.相交而不过圆心 | C.相切 | D.相离 |
圆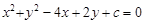 与直线
与直线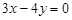 相交于
相交于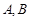 两点,圆心为
两点,圆心为 ,若
,若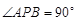 ,则
,则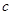 的值为( )
的值为( )
| A.8 | B.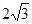 | C.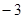 | D.3 |
过原点且倾斜角为 的直线被圆学
的直线被圆学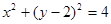 所截得的弦长为(科网 )
所截得的弦长为(科网 )
A.2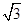 | B.2 | C.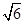 | D.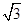 |
直线y=x+b与曲线x=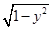 有且仅有一个公共点,则b的取值范围是( )
有且仅有一个公共点,则b的取值范围是( )
A.{b|b=± } } |
B.{b|-1<b≤1或b=- } } |
C.{b|-1≤b≤ } } |
D.{b|- <b<1} <b<1} |
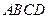 的两条对角线相交于点
的两条对角线相交于点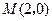 ,
, 边所在直线的方程为
边所在直线的方程为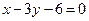 , 点
, 点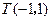 在
在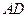 边所在直线上.求:
边所在直线上.求: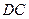 边所在的直线方程.
边所在的直线方程. 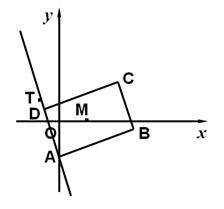
 B.2 C.3 D.2
B.2 C.3 D.2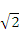 ,0)引直线ι与曲线
,0)引直线ι与曲线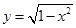 交于A,B两点 ,O为坐标原点,当△AOB的面积取最大值时,直线ι的斜率等于( )
交于A,B两点 ,O为坐标原点,当△AOB的面积取最大值时,直线ι的斜率等于( )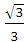 B.-
B.-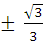 D-
D-