题目内容
在 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且 成等差数列.
成等差数列.
(1)求角 的大小;
的大小;
(2)若 ,求
,求 边上中线长的最小值.
边上中线长的最小值.
(1)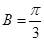 ;(2)
;(2)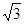 .
.
解析试题分析:(1)由已知, ,利用正弦定理,将边
,利用正弦定理,将边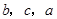 代换成
代换成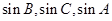 ,再利用两角和正弦公式求
,再利用两角和正弦公式求 ;(2)设
;(2)设 边上的中点为
边上的中点为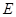 ,利用三边
,利用三边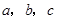 用余弦等量将中线
用余弦等量将中线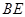 表示出来,再用基本不等式求最小值.
表示出来,再用基本不等式求最小值.
(1)由题意得: ,
,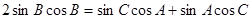 ,
,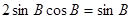 ,
,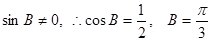 .
.
(2)设 边上的中点为
边上的中点为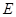 ,
,
由余弦定理得: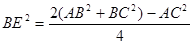
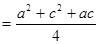
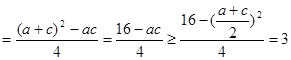 ,
,
当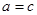 时取到”=”所以
时取到”=”所以 边上中线长的最小值为
边上中线长的最小值为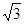 .
.
考点:1、正弦定理;2、余弦定理;3、两角和与差的正弦公式;4、基本不等式.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且
,且 ,
, ,
, .
. 与边
与边 在
在 方向上的投影.
方向上的投影. 北偏东
北偏东 方向的
方向的 处有一电视塔,火车站正东方向的
处有一电视塔,火车站正东方向的 处有一小汽车,测得
处有一小汽车,测得 距离为31
距离为31 ,该小汽车从
,该小汽车从 处,测得离电视塔21
处,测得离电视塔21 中,
中, 分别是
分别是 所对的边,
所对的边, ,
, ,三角形的面积为
,三角形的面积为 ,
, 的大小; (2)求
的大小; (2)求 的值.
的值.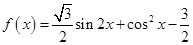 .
.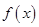 的最小正周期及在区间
的最小正周期及在区间 的最大值;
的最大值; 中,
中, 、
、 、
、 所对的边分别是
所对的边分别是 、
、 、
、 ,
, ,
, ,求
,求 周长
周长 的最大值.
的最大值. ,
, .
. 的值.
的值. 中,角
中,角 所对的边分别为
所对的边分别为 ,点
,点 在直线
在直线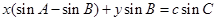 上.
上.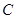 的值;
的值; ,且
,且 ,求
,求 .
. 中,
中, 的对边分别为
的对边分别为 且
且 .
. 的形状,并求
的形状,并求 的取值范围;
的取值范围; 分别在
分别在 上运动,
上运动, ,若直线
,若直线 直线
直线 ,且相交于点
,且相交于点 ,求
,求 间距离的取值范围.
间距离的取值范围.
 中,内角
中,内角 对边的长分别是
对边的长分别是 ,且
,且 .
. ,求
,求 ;
; ,求
,求