题目内容
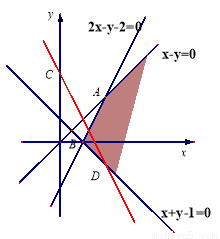
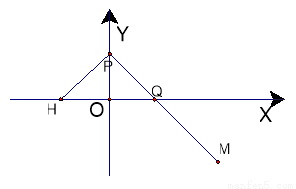
如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点, M为CD的中点.
M为CD的中点.

(1)求点M的轨迹方程;
(2)过M作AB的垂线,垂足为N,若存在正常数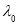 ,使
,使 ,且P点到A、B 的距离和为定值,求点P的轨迹E的方程;
,且P点到A、B 的距离和为定值,求点P的轨迹E的方程;
(3)过 的直线与轨迹E交于P、Q两点,求
的直线与轨迹E交于P、Q两点,求 面积的最大值.
面积的最大值.
(1)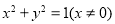 (2)
(2)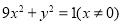 (3)
(3)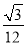
【解析】
试题分析:(1)求动点轨迹方程的步骤,一是设动点坐标M(x, y),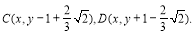 二是列出动点满足的条件
二是列出动点满足的条件 ,三是化简,
,三是化简,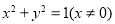 ,四是去杂,x≠0;(2)涉及两个动点问题,往往是通过相关点法求对应轨迹方程,设P(x, y),则
,四是去杂,x≠0;(2)涉及两个动点问题,往往是通过相关点法求对应轨迹方程,设P(x, y),则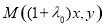 ,代入M的轨迹方程有
,代入M的轨迹方程有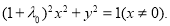 ,利用椭圆定义解出
,利用椭圆定义解出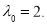 相关点法也叫转移法,即将未知转移到已知,用未知点坐标表示已知点坐标,是一种化归思想,(3)直线与椭圆位置关系,一般先分析其几何性,再用代数进行刻画.本题中的三角形可分解为两个同底三角形,底长都为,所以三角形面积最大值决定于高,即横坐标差的绝对值,这可结合韦达定理进行列式分析
相关点法也叫转移法,即将未知转移到已知,用未知点坐标表示已知点坐标,是一种化归思想,(3)直线与椭圆位置关系,一般先分析其几何性,再用代数进行刻画.本题中的三角形可分解为两个同底三角形,底长都为,所以三角形面积最大值决定于高,即横坐标差的绝对值,这可结合韦达定理进行列式分析
试题解析:【解析】
(1)设点M的坐标为M(x, y)(x≠0),则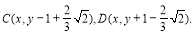
又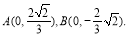 由AC⊥BD有
由AC⊥BD有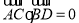 ,即
,即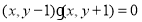 ,
,
∴x2+y2=1(x≠0). (4分)
(2)设P(x, y),则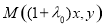 ,代入M的轨迹方程有
,代入M的轨迹方程有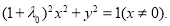
即 ,∴P的轨迹为椭圆(除去长轴的两个端点).
,∴P的轨迹为椭圆(除去长轴的两个端点).
要P到A、B的距离之和为定值,则以A、B为焦点,故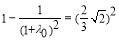 .
.
∴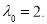 从而所求P的轨迹方程为
从而所求P的轨迹方程为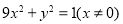 . 9分
. 9分
(3)易知l的斜率存在,设方程为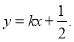 联立9x2+y2=1,有
联立9x2+y2=1,有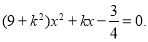
设P(x1,y1),Q(x2,y2),则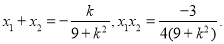
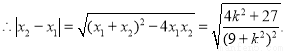 令
令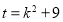 ,则
,则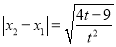 且
且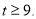
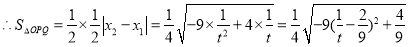 ,
,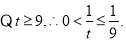
所以当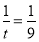 ,即
,即 也即
也即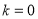 时,
时,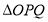 面积取最大值,最大值为
面积取最大值,最大值为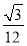 . 12分
. 12分
考点:直接法求轨迹方程,相关点法求轨迹方程,直线与椭圆位置关系

练习册系列答案
相关题目