题目内容
3.已知圆C经过三个点A(4,1),B(6,-3),C(-3,0).(1)求圆C的标准方程;
(2)过点M(-4,-2)作圆C的切线,求切线的方程.
分析 (1)设出圆的一般式方程,把三个点A(4,1),B(6,-3),C(-3,0)的坐标代入,求得D、E、F的值,即可求得圆的方程.
(2)分类讨论,利用圆心到直线的距离等于半径即可得出结论.
解答 解:(1)设圆C的一般方程为x2+y2+Dx+Ey+F=0,
因为点A(4,1),B(6,-3),C(-3,0)在所求的圆上,
所以$\left\{\begin{array}{l}{17+4D+E+F=0}\\{45+6D-3E+F=0}\\{9-3D+F=0}\end{array}\right.$,
所以D=-2,E=6,F=-15,
所以圆C的方程为x2+y2-2x+6y-15=0,标准方程为(x-1)2+(y+3)2=25;
(2)直线的斜率不存在时,直线方程为x=-4,满足题意;
设切线方程为y+2=k(x+4),即kx-y+4k-2=0,
所以圆心到直线的距离d=$\frac{|k+3+4k-2|}{\sqrt{{k}^{2}+1}}$=5,
所以k=$\frac{12}{5}$,
所以直线方程为y=-2+$\frac{12}{5}$×(x+4)=$\frac{12}{5}x+\frac{38}{5}$,
综上所述,切线的方程为y=$\frac{12}{5}x+\frac{38}{5}$或x=-4.
点评 本题主要考查用待定系数法求圆的方程,点到直线的距离公式的应用,属于中档题.

练习册系列答案
相关题目
13.已知函数y=logax3,下列哪个函数与其相同( )
| A. | y=(logax)3 | B. | y=loga2x | C. | y=log2ax | D. | y=3logax |
18.已知函数f(x)是R奇函数,在(0,+∞)是增函数且f(1)=0,则f(log2a)>0的a的取值范围是( )
| A. | $\frac{1}{2}$<a<1或a>2 | B. | 0$<a<\frac{1}{2}$ | C. | 0$<a<\frac{1}{2}$或a>2 | D. | a>2 |
8.已知a=${0.7}^{\frac{1}{3}}$,b=${0.6}^{-\frac{1}{3}}$,c=log20.5,则a,b,c的大小关系是( )
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | b<a<c |
3.执行如图的框图,若输出结果为2,则输入的实数x的值是( )
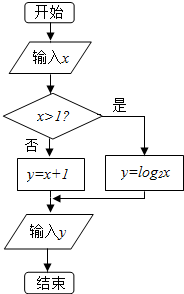

| A. | $\frac{3}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 4 |