题目内容
设函数f（x）=|x+1|+|x+2|+…+|x+2010|+|x-1|+|x-2|+…+|x-2010|（x∈R）四位同学研究得出如下四个命题，其中真命题的有____个
①f（x）是偶函数；
②f（x）在（0，+∞）单调递增；
③不等式f（x）＜2010×2011的解集为∅；
④关于实数a的方程f（a2-3a+2）=f（a-1）有无数解．
- A.1
- B.2
- C.3
- D.4
C
分析：对于①利用偶函数的定义可判断；对于②正确；对于③研究函数的最小值为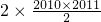
=2010×2011，故可判断；对于④由①②可知，a2-3a+2=a-1，∴a=1或a=3，故可得结论
解答：对于①f（-x）=f（x）∴正确；对于②正确；对于③，∵当x=0时，函数的最小值为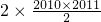=2010×2011，故正确对于④由①②可知，a2-3a+2=a-1，∴a=1或a=3，故④错，
故选C．
点评：本题主要考查命题真假的判断，解题的关键是正确理解函数，研究其性质．
分析：对于①利用偶函数的定义可判断；对于②正确；对于③研究函数的最小值为
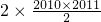=2010×2011，故可判断；对于④由①②可知，a2-3a+2=a-1，∴a=1或a=3，故可得结论解答：对于①f（-x）=f（x）∴正确；对于②正确；对于③，∵当x=0时，函数的最小值为
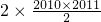=2010×2011，故正确对于④由①②可知，a2-3a+2=a-1，∴a=1或a=3，故④错，故选C．
点评：本题主要考查命题真假的判断，解题的关键是正确理解函数，研究其性质．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
设函数f（x）的定义域为A，若存在非零实数t，使得对于任意x∈C（C⊆A），有x+t∈A，且f（x+t）≤f（x），则称f（x）为C上的t低调函数．如果定义域为[0，+∞）的函数f（x）=-|x-m2|+m2，且 f（x）为[0，+∞）上的10低调函数，那么实数m的取值范围是（ ）
| A、[-5，5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|