题目内容
△ABC中,
=(1+cosα,sinα),
=(cosα,1+sinα),α∈(0,
).
(1)求:|
|及∠C的大小;
(2)求:△ABC的面积S的最大值.
| AC |
| BC |
| π |
| 2 |
(1)求:|
| AB |
(2)求:△ABC的面积S的最大值.
分析:(1)由已知中向量
=(1+cosα,sinα),
=(cosα,1+sinα),我们可以计算出向量
的坐标,代入向量坐标公式,即可求出答案,再由cosC=
结合三角函数恒等变换,我们求出C的余弦值,进而求出C的大小.
(2)由已知中向量
=(1+cosα,sinα),
=(cosα,1+sinα),我们求出cosA,代入S=
|
|•|
|•sinA,根据α∈(0,
),利用换元法,易求出函数的最值,进而得到△ABC的面积S的最大值.
| AC |
| BC |
| AB |
| ||||
|
|
(2)由已知中向量
| AC |
| BC |
| 1 |
| 2 |
| AB |
| AC |
| π |
| 2 |
解答:解:(1)∵
=(1+cosα,sinα),
=(cosα,1+sinα),
∴
=
-
=(1,-1)
∴|
|=
,
∵cosC=
=
=
C=45°;
(2)∵|
|=
,
∴
•
=1+cosα-sinα,
∴cosA=
=
∴cos2A=
=
,
∴sinA=
,
∴S=
|
|•|
|•sinA
=
,α∈(0,
),
设t=sinα+cosα,则sinα•cosα=
,t∈(1,
],
∴S=
=
,
当t=
时,S取最大值
.
∴Smax=
.
| AC |
| BC |
∴
| AB |
| AC |
| BC |
∴|
| AB |
| 2 |
∵cosC=
| ||||
|
|
| 1+sinα+cosα | ||
2
|
| ||
| 2 |
C=45°;
(2)∵|
| AC |
| 2+2cosα |
∴
| AB |
| AC |
∴cosA=
| ||||
|
|
| 1+cos-sinα | ||
2
|
∴cos2A=
| 1-sinα+cos-sinα•cos |
| 2(1+cosα) |
| 1-sinα |
| 2 |
∴sinA=
|
∴S=
| 1 |
| 2 |
| AB |
| AC |
=
|
| π |
| 2 |
设t=sinα+cosα,则sinα•cosα=
| t2-1 |
| 2 |
| 2 |
∴S=
|
| t +1 |
| 2 |
当t=
| 2 |
| ||
| 2 |
∴Smax=
| ||
| 2 |
点评:本题考查的知识点是向量数量积,向量夹角公式,三角函数的最值,三角函数的恒等变换,是平面向量与三角函数比较综合的考查,难度较大.解答时,要注意已知中各向量对应的有向线段是三角形的边.

练习册系列答案
相关题目
 如图,在△ABC中,AC=BC,AB=2,O为AB的中点,沿OC将△AOC折起到△A′OC的位置,使得直线A′B与平面ABC成30°角.
如图,在△ABC中,AC=BC,AB=2,O为AB的中点,沿OC将△AOC折起到△A′OC的位置,使得直线A′B与平面ABC成30°角.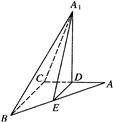 在Rt△ABC中,AC=4,BC=3,∠C=90°,D,E分别为AC,AB边上的点,且DE∥BC,沿DE将△ADE折起(记为△A1DE),使二面角A1-DE-B为直二面角.
在Rt△ABC中,AC=4,BC=3,∠C=90°,D,E分别为AC,AB边上的点,且DE∥BC,沿DE将△ADE折起(记为△A1DE),使二面角A1-DE-B为直二面角.