题目内容
11.已知(x+1)5(2x-1)3=a0+a1x+a2x2+…+a8x8,其中a0,a1,a2,…,a8∈R,则a1+a2+a3+…+a8=33.分析 在所给的等式中,令x=0可得a0的值;令x=1,可得a0+a1+a2+a3+…+a8的值,从而求得a1+a2+a3+…+a8的值.
解答 解:对于(x+1)5(2x-1)3=a0+a1x+a2x2+…+a8x8,令x=0可得a0=-1,
在(x+1)5(2x-1)3=a0+a1x+a2x2+…+a8x8,令x=1,
可得a0+a1+a2+a3+…+a8=32,∴a1+a2+a3+…+a8=33.
故答案为:33.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于基础题.

练习册系列答案
相关题目
3.已知实数x、y满足不等式组$\left\{\begin{array}{l}{x-3y+1≤0}\\{x+y-3≥0}\\{x≥0}\end{array}\right.$,则x2+y2的最小值是( )
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{9}{2}$ | C. | 5 | D. | 9 |
20.已知集合A={0,b},B={x∈Z|x2-3x<0},若A∩B≠∅,则b等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 1或2 |
7.已知i是虚数单位,复数$\frac{1+i}{2-i}$=( )
| A. | $\frac{1}{5}-\frac{3}{5}$i | B. | $\frac{3}{5}+\frac{1}{5}$i | C. | $\frac{1}{3}+\frac{2}{3}$i | D. | $\frac{1}{5}+\frac{3}{5}$i |
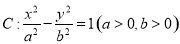 的右焦点为
的右焦点为 ,直线
,直线 与双曲线
与双曲线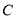 的渐近线在第一象限的交点为
的渐近线在第一象限的交点为 为坐标原点,若
为坐标原点,若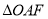 的面积为
的面积为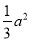 ,则双曲线
,则双曲线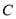 的离心率为( )
的离心率为( ) B.
B.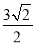
 D.
D.
 ,
,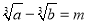 ,
,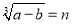 ,则有( )
,则有( )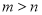 B.
B.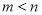
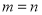 D.
D.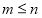
 为
为 内一点,满足
内一点,满足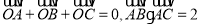 ,且
,且 ,则
,则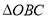 的面积为____________.
的面积为____________.