题目内容
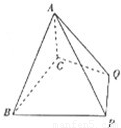
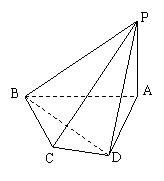
 如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4.
如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4.(1)若点G是AE的中点,求证:AC∥平面BDG;
(2)试问点F在线段AB上什么位置时,二面角B-CE-F的余弦值为
| 3 |
| 13 |
| 13 |
分析:(Ⅰ)利用三角形的中位线定理和线面平行的判定定理即可证明;
(2)建立空间直角坐标系,求平面BCE和CEF的法向量,利用向量法求二面角的大小,解方程即可得出.
(2)建立空间直角坐标系,求平面BCE和CEF的法向量,利用向量法求二面角的大小,解方程即可得出.
解答:解:(1)证明:连接CE、BD,设CE∩BD=O,连接OG,
由三角形的中位线定理可得:OG∥AC,
∵AC?平面BDG,OG?平面BDG,
∴AC∥平面BDG.
(2)∵平面ABC⊥平面BCDE,DC⊥BC,
∴DC⊥平面ABC,
∴DC⊥AC,
∵△ABC是正三角形,
∴取AC的中点M,连结MO,则MO∥CD,
∴MO⊥面ABC,
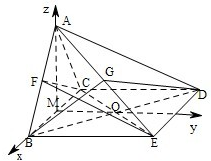
以M为坐标原点,以MB,M0,MA分别为x,y,z轴,建立空间直角坐标系,
∵AB=2,AD=4,∴AM=
,
∴B(1,0,0),C(-1,0,0),A(0,0,
),
在Rt△ACD中,CD=
=
=
=2
.
∴BE=CD=2
,即E(1,2
,0)
则
=(-1,0,
),
∵点F在线段AB上,
∴设BF=xBA,(0≤x≤1)
则
=x
∴F(1-x,0,
x),则
=(2,2
,0),
=(2-x,0,
x),
设面CEF的法向量为
=(a,b,c),
则由
得,
,
令a=
,则b=-1,c=
,即
=(
,-1,
),
平面BCE的法向量为
=(0,0,1),
二面角B-CE-F的余弦值为
=
,
即
=
,
∴
=
,
平方得
=
,解得:(
)2=9,
解得x=-1(舍去)或x=
.
即F是线段AB的中点时,二面角B-CE-F的余弦值为
.
由三角形的中位线定理可得:OG∥AC,
∵AC?平面BDG,OG?平面BDG,
∴AC∥平面BDG.
(2)∵平面ABC⊥平面BCDE,DC⊥BC,
∴DC⊥平面ABC,
∴DC⊥AC,
∵△ABC是正三角形,
∴取AC的中点M,连结MO,则MO∥CD,
∴MO⊥面ABC,
以M为坐标原点,以MB,M0,MA分别为x,y,z轴,建立空间直角坐标系,
∵AB=2,AD=4,∴AM=
| 3 |
∴B(1,0,0),C(-1,0,0),A(0,0,
| 3 |
在Rt△ACD中,CD=
| AD2-AC2 |
| 42-22 |
| 12 |
| 3 |
∴BE=CD=2
| 3 |
| 3 |
则
| BA |
| 3 |
∵点F在线段AB上,
∴设BF=xBA,(0≤x≤1)
则
| BF |
| BA |
∴F(1-x,0,
| 3 |
| CE |
| 3 |
| CF |
| 3 |
设面CEF的法向量为
| n |
则由
|
|
令a=
| 3 |
| x-2 |
| x |
| n |
| 3 |
| x-2 |
| x |

平面BCE的法向量为
| m |
二面角B-CE-F的余弦值为
|
| ||||
|
|
3
| ||
| 13 |
即
|
| ||||||
|
3
| ||
| 13 |
∴
(
| ||||
|
3
| ||
| 13 |
平方得
(
| ||
4+(
|
| 9 |
| 13 |
| x-2 |
| x |
解得x=-1(舍去)或x=
| 1 |
| 2 |
即F是线段AB的中点时,二面角B-CE-F的余弦值为
| 3 |
| 13 |
| 13 |
点评:本题主要考查直线和平面平行的判定定理,以及利用向量法解决二面角的大小问题,综合性较强,运算量较大.

练习册系列答案
相关题目
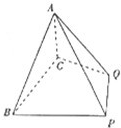 (2012•南宁模拟)如图:四棱锥A-BCQP中,二面角A-BC-P为90°,且∠BAC=∠BCQ=90°,∠CBP=45°BP+AP=
(2012•南宁模拟)如图:四棱锥A-BCQP中,二面角A-BC-P为90°,且∠BAC=∠BCQ=90°,∠CBP=45°BP+AP=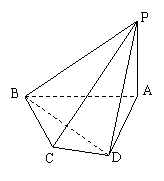
 BC,AB=AC=
BC,AB=AC= B.
B.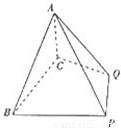
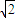 BC,AB=AC=
BC,AB=AC=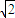 B.
B.