题目内容
 的定义域是 .
的定义域是 .
【答案】分析:根据使函数的解析式有意义的原则,我们可以构造出关于x的三角不等式,根据余弦函数的性质,我们解不等式即可得到函数的定义域.
解答:解:要使函数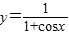 的解析式有意义
的解析式有意义
自变量x须满足:1+cosx≠0
即cosx≠-1
x≠(2k+1)π,k∈Z
故函数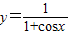 的定义域是{x|x≠(2k+1)π,k∈Z}
的定义域是{x|x≠(2k+1)π,k∈Z}
故答案为:{x|x≠(2k+1)π,k∈Z}
点评:本题考查的知识点是函数的定义域,余弦函数的性质,其中根据使函数的解析式有意义的原则,构造出关于x的三角不等式,是解答本题的关键.
解答:解:要使函数
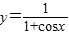 的解析式有意义
的解析式有意义自变量x须满足:1+cosx≠0
即cosx≠-1
x≠(2k+1)π,k∈Z
故函数
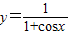 的定义域是{x|x≠(2k+1)π,k∈Z}
的定义域是{x|x≠(2k+1)π,k∈Z}故答案为:{x|x≠(2k+1)π,k∈Z}
点评:本题考查的知识点是函数的定义域,余弦函数的性质,其中根据使函数的解析式有意义的原则,构造出关于x的三角不等式,是解答本题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
已知函数f(x+1)=log2(2x+1),那么f(x)的定义域是( )
A、{x|x>-
| ||
B、{x|x>
| ||
C、{x|x>-
| ||
| D、{x|x>0} |