题目内容
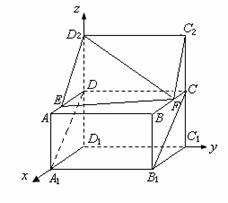
(本小题满分10分)如图,正四棱柱ABCD—A1B1C1D1的底面边长为1,侧棱长为t,点D1关于点D的对称点为D2,点C1关于点C的对称点为C2,点E、F分别在线段AD和BC上,且DE=BF=![]() (0<
(0<![]() <1).
<1).
(1)若![]() ,t=1,求直线D2F与直线B1C所成角
,t=1,求直线D2F与直线B1C所成角![]() 。
。
(2)是否存在实数![]() 和t,使得平面EFD2⊥平面A1B1CD?若存在,求出
和t,使得平面EFD2⊥平面A1B1CD?若存在,求出![]() 和t;若不存在,说明理由.
和t;若不存在,说明理由.
(3)若t=1,![]() <
<![]() <1,设直线C2F与平面EFD2所成角为
<1,设直线C2F与平面EFD2所成角为![]() ,求证:.
,求证:.![]() .
.

解:在建立如图所示的坐标系中,
A1(1,0,0) B1(1,1,0) C1(0,1,0) D1(0,0,0)
A(1,0,t) B(1,1,t) C(0,1,t) D(0,0,t)
E(λ,0,t) F(1-λ,1,t) C2(0,1,2t) D2(0,0,2t)
![]() =(1-λ,1,-t),
=(1-λ,1,-t),![]() =(-1,0,t)
=(-1,0,t)
(1)![]() =(
=(![]() ,1,-1),
,1,-1),![]() =(-1,0,1)
=(-1,0,1)
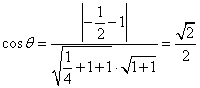 ,
,
∴所成角![]() ………………………(3分)
………………………(3分)
(2)![]() =(λ,0,-t),设平面EFD2的法向量为
=(λ,0,-t),设平面EFD2的法向量为![]() (1,p,q)则
(1,p,q)则
![]() ,∴
,∴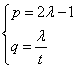 ,即
,即![]() =(1,2λ-1,
=(1,2λ-1,![]() )
)
易求平面A1B1CD的法向量为![]() (1,0,
(1,0,![]() ),
),
∴![]() ·
·![]() 1+
1+![]() ,∵
,∵![]() ,∴1+
,∴1+![]() ≠0,∴两平面不可能垂直. …………(6分)
≠0,∴两平面不可能垂直. …………(6分)
(3)∵![]() ,
,![]() ,
,
∴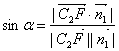
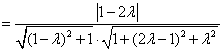 .
.
令![]() ,则
,则![]() ,
,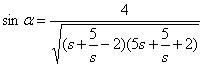 ,
,
当![]() 时,
时,![]() ,
,
∴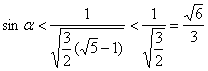 .………………………………………………(10分)
.………………………………………………(10分)

练习册系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,