题目内容
(本题满分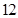 分)(理科)在线段AD上任取不同于A,D的两点B,C,在B,C处折断此线段得到一条折线。求此折线能构成三角形的概率。
分)(理科)在线段AD上任取不同于A,D的两点B,C,在B,C处折断此线段得到一条折线。求此折线能构成三角形的概率。
【答案】
解法1:设AD长为1,折断后三段长分别是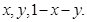 则
则 此不等式组表示的平面区域为如图1所示的
此不等式组表示的平面区域为如图1所示的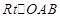 的内部。这样的点
的内部。这样的点 对应于试验的所有可能结果。
对应于试验的所有可能结果。
设“以 为边能构成三角形”为事件A,则A发生当且仅当
为边能构成三角形”为事件A,则A发生当且仅当 满足
满足 即图中
即图中 的内部。
的内部。
这是一个几何概型问题,故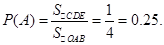
解法2:设AD长为1,AB,AC的长度分别为x,y。上于B,C在线段AD上,因而应有0≤x,y≤1。由此可见,点对(B,C)与正方形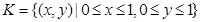 内的点(x,y)是一一对应的。
内的点(x,y)是一一对应的。
当x<y时,这时AB,BC,CD能构成三角形的充要条件是AB+BC>CD,BC+CD>AB,CD+AB>BC。因为AB=x,BC=y-x,CD=1-y,代入上面三式,得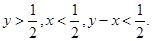 符合此条件的点(x,y)必落在
符合此条件的点(x,y)必落在 (图2)。同样地,当
(图2)。同样地,当 时,当且仅当点
时,当且仅当点 落在
落在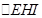 中时,AC,CB,BD能构成三角形。由几何概型的公式可知,所求的概率为
中时,AC,CB,BD能构成三角形。由几何概型的公式可知,所求的概率为
△GFE的面积+△EHI的面积
正方形K的面积
=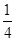
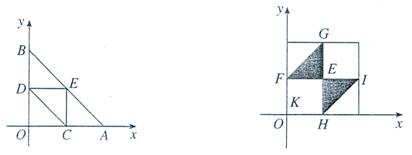
(图1) (图2)
【解析】略

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
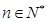 ,
,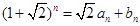 (
(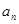 、
、 )。
)。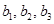 的值;
的值;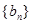 的各项均为奇数.
的各项均为奇数. .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.