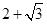题目内容
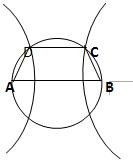 如图,以AB为直径的圆有一内接梯形ABCD,且AB∥CD.若双曲线C1以A、B为焦点,且过C、D两点,则当梯形的周长最大时,双曲线的离心率为
如图,以AB为直径的圆有一内接梯形ABCD,且AB∥CD.若双曲线C1以A、B为焦点,且过C、D两点,则当梯形的周长最大时,双曲线的离心率为
分析:设∠BAC=θ,作CE⊥AB于点E,则可表示出BC,EB,CD,进而可求得梯形的周长的表达式,根据二次函数的性质求得周长的最大值时θ的值,则AC和BC可求,进而根据双曲线的定义求得双曲线的长轴,进而利用e=
求得答案.
| c |
| a |
解答:解:设∠BAC=θ,作CE⊥AB于点E,
则BC=2Rsinθ,EB=BCcos(90°-θ)=2Rsin2θ,有CD=2R-4Rsin2θ,
梯形的周长l=AB+2BC+CD=2R+4Rsinθ+2R-4Rsin2=-4R(sinθ-
)2+5R.
当sinθ=
,即θ=30°时,l有最大值5R,这时,BC=R,AC=
R,a=
(AC-BC)=
(
-1)R,e=
=
+1.
故答案为
+1
则BC=2Rsinθ,EB=BCcos(90°-θ)=2Rsin2θ,有CD=2R-4Rsin2θ,
梯形的周长l=AB+2BC+CD=2R+4Rsinθ+2R-4Rsin2=-4R(sinθ-
| 1 |
| 2 |
当sinθ=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| c |
| a |
| 3 |
故答案为
| 3 |
点评:本题主要考查了双曲线的应用,双曲线的定义.考查了学生分析问题和解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
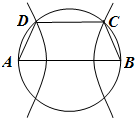 如图,以AB为直径的圆有一内接梯形ABCD,且AB∥CD.若双曲线以A、B为焦点,且过C、D两点,则当梯形的周长最大时,双曲线的离心率为( )
如图,以AB为直径的圆有一内接梯形ABCD,且AB∥CD.若双曲线以A、B为焦点,且过C、D两点,则当梯形的周长最大时,双曲线的离心率为( )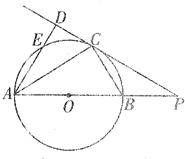 选修4-1:几何证明选讲
选修4-1:几何证明选讲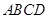 ,且
,且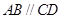 .若双曲线
.若双曲线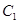 以A、B为焦点,且过C、D两点,则当梯形的周长最大时,双曲线的离心率为( ).
以A、B为焦点,且过C、D两点,则当梯形的周长最大时,双曲线的离心率为( ).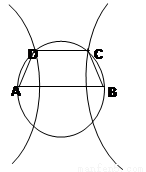
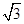 B.
B.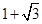 C.2 D.
C.2 D.