题目内容
已知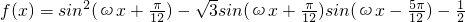 (ω>0)在区间
(ω>0)在区间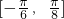 上的最小值为-1,则ω的最小值为________.
上的最小值为-1,则ω的最小值为________.

分析:由三角函数的倍角公式把
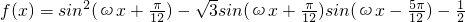 等价转化为y=
等价转化为y=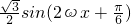 -
-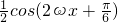 ,再由三角函数的和(差)角公式进一步等价转化为y=sin2ωx.因为x∈
,再由三角函数的和(差)角公式进一步等价转化为y=sin2ωx.因为x∈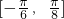 ,所以2ωx∈
,所以2ωx∈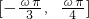 ,再由f(x)在区间
,再由f(x)在区间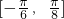 上的最小值为-1,得到
上的最小值为-1,得到 ,或
,或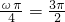 ,由此能够求出ω的最小值.
,由此能够求出ω的最小值.解答:∵ω>0,
∴
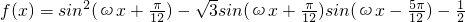
=
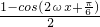 +
+
=
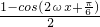 +
+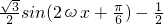
=
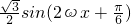 -
-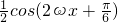
=sin2ωx.
∵x∈
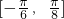 ,
,∴2ωx∈
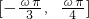 ,
,∵f(x)在区间
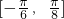 上的最小值为-1,
上的最小值为-1,∴
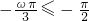 ,或
,或
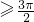 ,
,解得ω≥
 ,或ω≥6,
,或ω≥6,∴ω的最小值=
 .
.故答案为:
 .
.点评:本题考查正弦型曲线的图象和性质,综合性强,难度大,容易出错.解题时要认真审题,注意三角函数的倍角公式、和(差)角公式的灵活运用.

练习册系列答案
相关题目