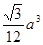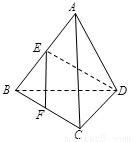题目内容
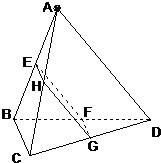 如图,在正三棱锥A-BCD中,∠BAC=30°,AB=a,平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于点E、F、G、H.
如图,在正三棱锥A-BCD中,∠BAC=30°,AB=a,平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于点E、F、G、H.
(1)判定四边形EFGH的形状,并说明理由.
(2)设P是棱AD上的点,当AP为何值时,平面PBC⊥平面EFGH,请给出证明.
解:(1)∵AD∥面EFGH,面ACD∩面EFGH=HG,AD?面ACD
∴HG∥EF.(2分)
同理EH∥FG,
∴四边形EFGH是平行四边形(3分)
∵三棱锥A-BCD是正三棱锥,
∴A在底面上的射影O是△BCD的中心,
∴DO⊥BC,
∴AD⊥BC,
∴HG⊥EH,四边形EFGH是矩形(5分)
(2)当AP= a时,平面PBC⊥平面EFGH.(7分)
a时,平面PBC⊥平面EFGH.(7分)
证明如下:
作CP⊥AD于P点,连接BP,
∵AD⊥BC,
∴AD⊥面BCP(10分)
∵HG∥AD,
∴HG⊥面BCP,HG?面EFGH?面BCP⊥面EFGH,
在Rt△APC中,∠CAP=30°,AC=a,
∴AP= a(12分)
a(12分)
分析:(1)先利用AD∥面EFGH?AD∥HG,同理EF∥FG?四边形EFGH是平行四边形.再利用AD⊥BC?HG⊥EH?四边形EFGH是矩形.
(2)作CP⊥AD于P点,连接BP,再由AD⊥BC?AD⊥面BCP,证得HG⊥面BCP?平面PBC⊥平面EFGH.然后在Rt△APC中,求出AP即可.
点评:本题考查平面和平面垂直的判定和性质.在证明面面垂直时,其常用方法是在其中一个平面内找两条相交直线和另一平面内的某一条直线垂直.
∴HG∥EF.(2分)
同理EH∥FG,
∴四边形EFGH是平行四边形(3分)
∵三棱锥A-BCD是正三棱锥,
∴A在底面上的射影O是△BCD的中心,
∴DO⊥BC,
∴AD⊥BC,
∴HG⊥EH,四边形EFGH是矩形(5分)
(2)当AP=
 a时,平面PBC⊥平面EFGH.(7分)
a时,平面PBC⊥平面EFGH.(7分)证明如下:
作CP⊥AD于P点,连接BP,
∵AD⊥BC,
∴AD⊥面BCP(10分)
∵HG∥AD,
∴HG⊥面BCP,HG?面EFGH?面BCP⊥面EFGH,
在Rt△APC中,∠CAP=30°,AC=a,
∴AP=
 a(12分)
a(12分)分析:(1)先利用AD∥面EFGH?AD∥HG,同理EF∥FG?四边形EFGH是平行四边形.再利用AD⊥BC?HG⊥EH?四边形EFGH是矩形.
(2)作CP⊥AD于P点,连接BP,再由AD⊥BC?AD⊥面BCP,证得HG⊥面BCP?平面PBC⊥平面EFGH.然后在Rt△APC中,求出AP即可.
点评:本题考查平面和平面垂直的判定和性质.在证明面面垂直时,其常用方法是在其中一个平面内找两条相交直线和另一平面内的某一条直线垂直.

练习册系列答案
相关题目
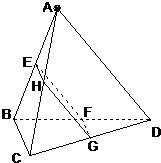 如图,在正三棱锥A-BCD中,∠BAC=30°,AB=a,平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于点E、F、G、H.
如图,在正三棱锥A-BCD中,∠BAC=30°,AB=a,平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于点E、F、G、H.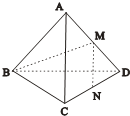 如图,在正三棱锥A-BCD中,M、N分别是AD、CD的中点,BM⊥MN,则正三棱锥的侧面与底面所成角的正切值为( )
如图,在正三棱锥A-BCD中,M、N分别是AD、CD的中点,BM⊥MN,则正三棱锥的侧面与底面所成角的正切值为( ) 如图,在正三棱锥A-BCD中,底面正三角形BCD的边长为2,点E是AB的中点,AC⊥DE,则正三棱锥A-BCD的体积是
如图,在正三棱锥A-BCD中,底面正三角形BCD的边长为2,点E是AB的中点,AC⊥DE,则正三棱锥A-BCD的体积是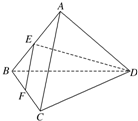 如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积是
如图,在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积是 ,则A—BCD的体积为 ( )
,则A—BCD的体积为 ( )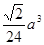 B.
B.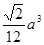
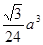 D.
D.