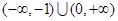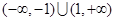题目内容
设A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0},其中x∈R,如果A∩B=B,求实数a的取值范围.
a=1或a≤-1
由A∩B=B得B⊆A,而A={-4,0},
Δ=4(a+1)2-4(a2-1)=8a+8,
当Δ=8a+8<0,即a<-1时,B=?,符合B⊆A;
当Δ=8a+8=0,即a=-1时,B={0},符合B⊆A;
当Δ=8a+8>0,即a>-1时,B中有两个元素,而B⊆A={-4,0};
∴B={-4,0}得a=1.∴a=1或a≤-1.
Δ=4(a+1)2-4(a2-1)=8a+8,
当Δ=8a+8<0,即a<-1时,B=?,符合B⊆A;
当Δ=8a+8=0,即a=-1时,B={0},符合B⊆A;
当Δ=8a+8>0,即a>-1时,B中有两个元素,而B⊆A={-4,0};
∴B={-4,0}得a=1.∴a=1或a≤-1.
练习册系列答案
名校课堂系列答案
相关题目
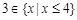
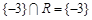
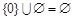
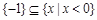
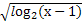},B={y|y=
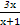},则A∩B=( )
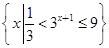，B＝{x|log2x≤1}，则A∪B等于( )
，
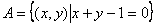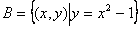，则
.
，
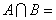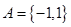，则集合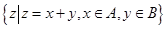
中的元素的个数为（ ）
，
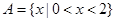，则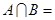
（ ）
